Analyse Bivariée
M2 IGAST
Martin Cubaud
LASTIG-UGE-IGN/ENSG
2025-2026

Introduction et rappels
Sources et références
- Ce cours reprend le cheminement des cours M2 IGAST 2020 de Paul Chapron et 2017 d’Élodie Buard
- Probabilités, analyse de données et statistiques , Gilbert Saporta, Editions TECHNIP, 2011
- Nombreuses ressources en ligne : http://www.foad-mooc.auf.org/IMG/pdf/424B_-Application_des_methodes_statistiques_d_analyse.pdf
- et wikipedia !
Rappel : Deux familles statistiques
statistiques inférentielles
Pour répondre à la question : «A partir d’un échantillon , que peut-on attendre (inférer) de la population ?»
- Modèles, estimateurs… : régression, estimation, extrapolation
- Liaisons statistiques : corrélation, covariance
- test statistiques, notions de probabilités
- e.g. sondages, rencensement, intervalle de confiance , prédictions…
Rappel : Deux familles statistiques
statistiques descriptives
Pour résumer, synthétiser, rendre intelligible, les propriétés d’une population à partir des variables qui décrivent les individus et la répartition de leurs valeurs.
- Graphiques (histogrammes, boxplots…)
- Mesures (fréquences, distributions, moments…)
- classification, ACP…
Rappel : vocabulaire
Population : Ensemble d'individus
“données”, “corpus”, “échantillon”, “data”
Individu : Unité statistique élémentaire = «les lignes du tableau»
Variables : Caractéristiques, propriétés d’un individu, mesurées par des enquêtes, des observations… = «les colonnes du tableau»
L’objet du cours : l’ Analyse Bivariée
Objectif : Analyser le lien entre deux variables, par exemple :
lien entre deux variables quantitatives
“nombre d’habitants et nombre de lignes de bus par département”
“nombre de lignes de bus en 1998 et en 2018”
lien entre deux variables qualitatives
“couleur des yeux et port de lunettes”
lien entre une variable quantitative, une variable qualitative
“taille et couleur des yeux”
Mise en garde
⚠ Une liaison, même très forte, entre deux variables, n’indique pas la causalité! ⚠
Erreur très courrante, très tentante.
© TylerVigen http://tylervigen.com/spurious-correlations
Analyse bivariée avec des données spatiales
Données spatiales
- Individus restreints spatialement (selection spatiale)
- variables “géographique” (e.g. lieu de résidence) renseignées pour les individus
prise en compte des distances ? → modèle gravitaire
Données localisées
- Auto-corrélation spatiale (Moran’s I)
- Geographicaly Weighted Regression (GWR) ≈ regression linéaire avec prise en compte de la distance entre individus
Régression linéaire
Première étape
Toujours en premier : regarder l'aspect des données avec des graphiques (exploration visuelle)
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
pd.plotting.scatter_matrix(df, figsize=[20, 10], s=150)data(iris)
plot(iris)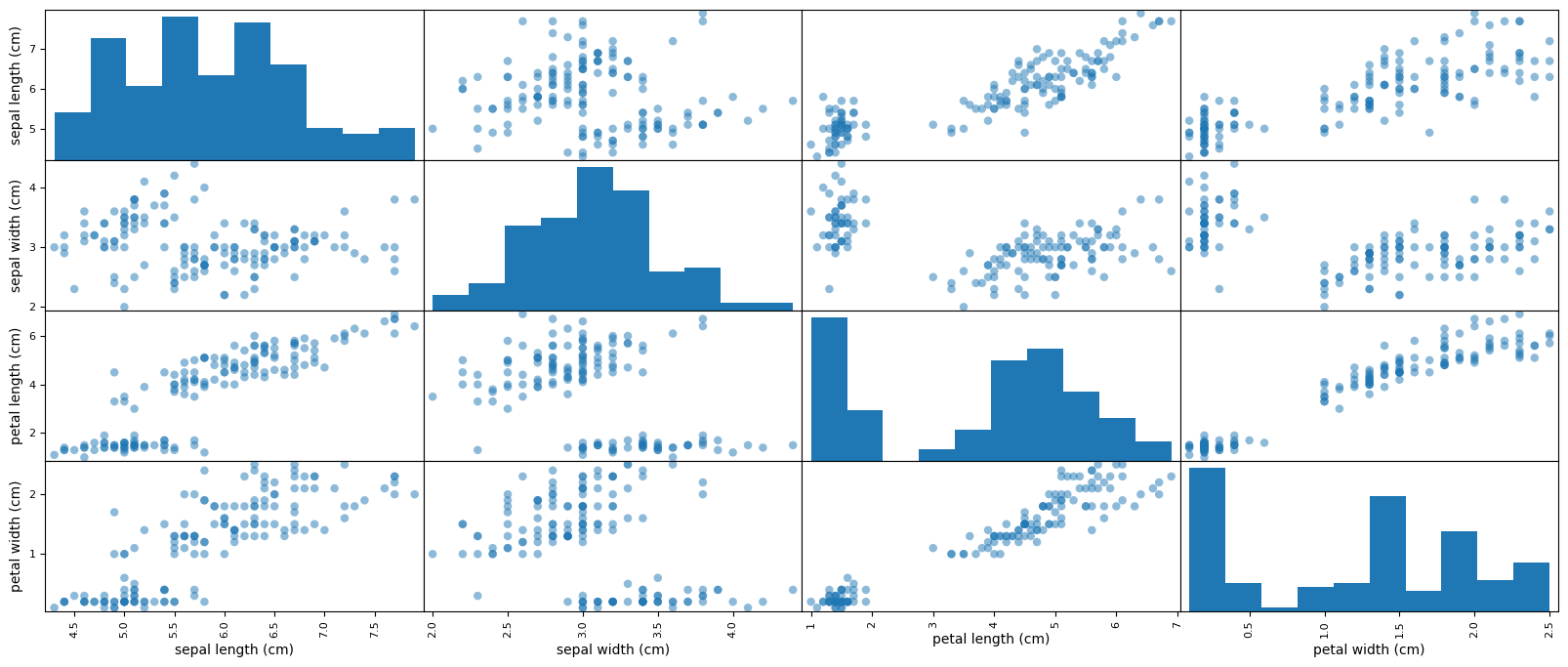
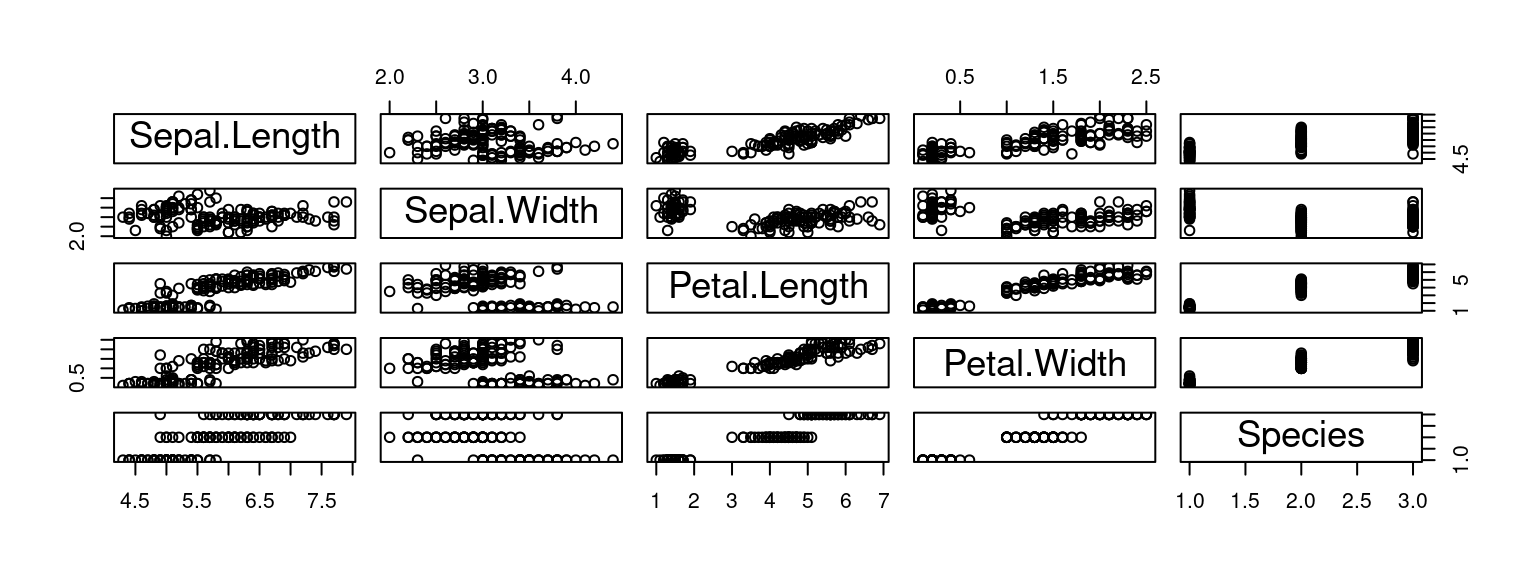
Existe-t-il un lien entre les variables ?
différentes formes de relations entre variables
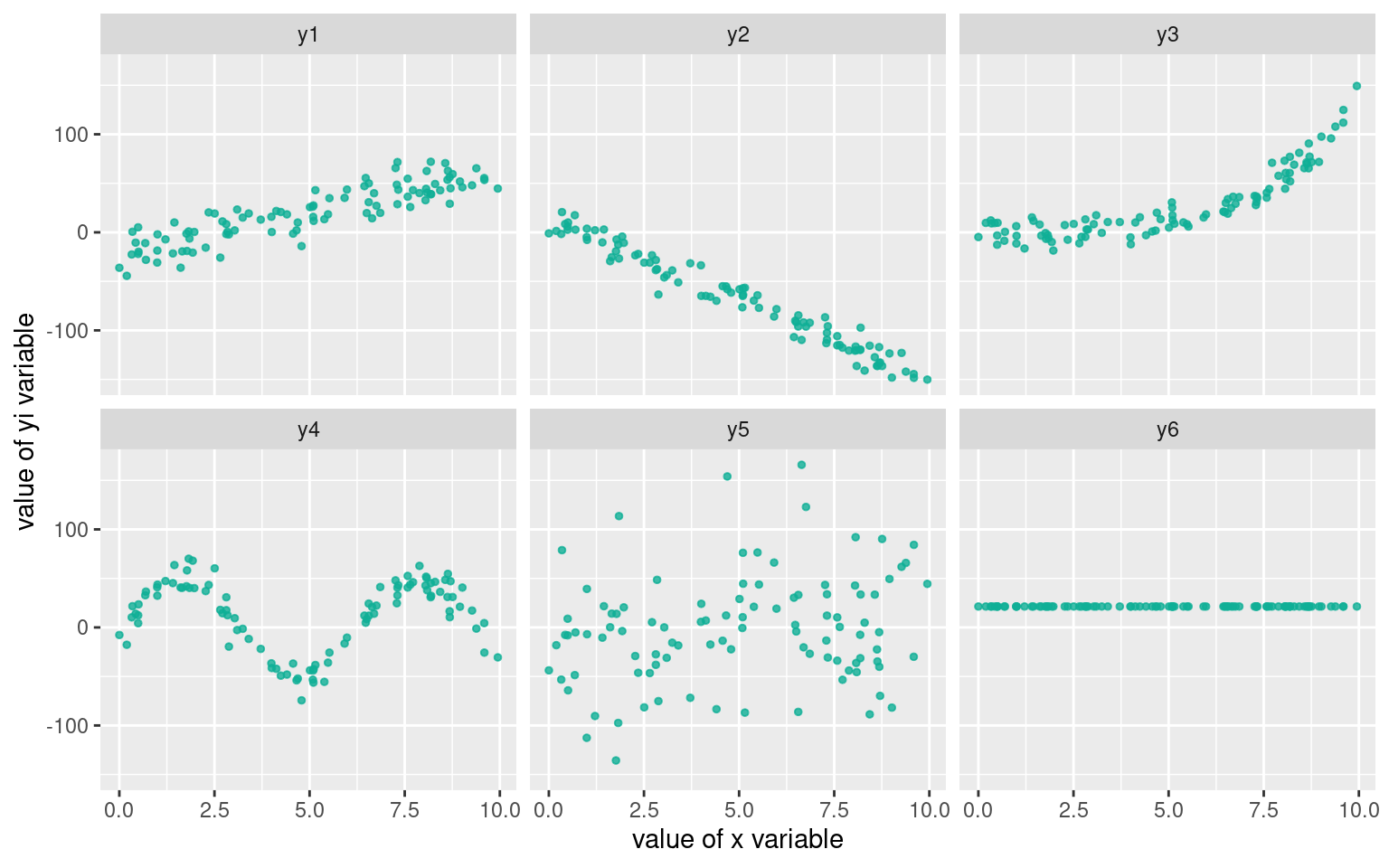
En pratique, les formes sont beaucoup moins régulières.
Les étapes
- Tracer le nuage de points
- Existe-t-il une relation ?
- Est-elle de forme linéaire ? De quel sens ?
- Si la liaison est de forme linéaire → faire une régression
- Si la liaison est non linéaire, est-elle monotone ? De forme connue ?→ Proposer un modèle
5bis. Réaliser un modèle LOESS avec prudence (uniquement descriptif , aucun pouvoir de généralisation)
cf le blog de Lise Vaudor [http://perso.ens-lyon.fr/lise.vaudor/regression-loess/]
Régression linéaire
Si la forme du nuage de points s’y prête, on peut faire une régression linéaire (aussi appelé ajustement linéaire).
On cherche la droite qui «passe au mieux» (=ajustée) dans le nuage de points de deux variables quantitatives $V_1$ et $V_2$, qui permet de visualiser :
Régression linéaire
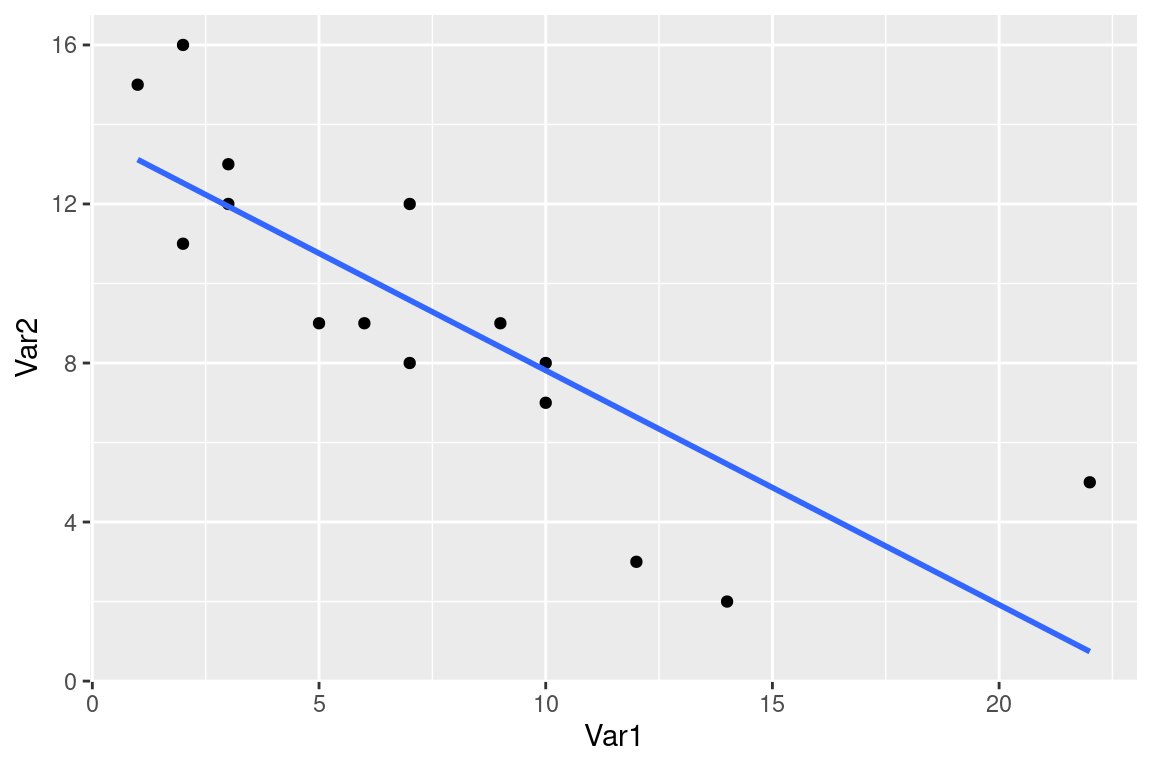
«Droite qui passe au mieux» = qui minimise la somme des écarts quadratiques entre la droite et les points du nuage.
Régression linéaire : le modèle
L’équation de la droite est un modèle linéaire de la relation statistique qui lie $V_1$ et $V_2$;
Ici le modèle est : $\hat{V}_2 = a V_1 + b$
$a$ et $b$ sont les paramètres ou coefficients du modèle.
Si la régression linéaire est avérée, alors pour un individu $i$ dont on connait $V_{1}i$, on infère la valeur $V_{2}i$ par le modèle : $\hat{V}_2i=a V_1i+b$
On dit aussi que $V_1$ explique $V_2$, ou que le modèle prédit $V_2$ à partir de $V_1$ (on note les valeurs prédites $\hat{V}_2$)
La grande question
Comment déterminer qu’une régression linéaire est «correcte» ?
Comment evaluer la “validité” du modèle linaire ?
En pratique, il faut réunir deux critères :
- des coefficients avec des p-values associées faibles (e.g. <0.05) ↔ “on a peu de chances de se tromper”
- un $R²$ élevé ↔ “le modèle prédit bien les observations”
Le $R²$
$R^2 \in [0, 1]$ est le coefficient de détermination linéaire.
Donne la qualité de prédiction de la régression.
“Proche de 1”" ≡ “très bonne qualité”
C’est le pourcentage de “variation” de $V_2$ due à la “variation” de $V_1$
Le $R²$
Défini par $R^2 = 1-\dfrac{\sum_{i=1}^n\left(y_i-\hat{y_i}\right)^2}{\sum_{i=1}^n\left(y_i-\bar y\right)^2} $
si on note $\hat{V}_2$ les valeurs de $V_2$ prédites par le modèle linéaire, alors :
$R^2 = cor(V_2, \hat{V}_2)^2$
(au sens de la corrélation de Pearson)
La p-value
Elle peut s’interpréter comme «la probabilité d’avoir un résultat de regression identique avec deux variables véritablement indépendantes»
La p-value est associée à la notion d’hypothèses nulle. Ici , l’hypothèse nulle est “les deux séries sont indépendantes”.
La p-value
Plus grossièrement : la p-value est le pourcentage de chances de se tromper en rejetant l’hypothèse nulle,
c'est-à-dire
se tromper en considérant que les deux séries ne sont pas indépendantes et qu’il existe une relation entre les deux (ici, linéaire car nous testons un modèle linéaire).
L'hypothèse nulle
$H_0$ : «les deux variables sont indépendantes»
- conserver $H_0$ : considérer les deux variables comme indépendantes
- rejeter $H_0$ : considérer les deux variables comme dépendantes = ayant une relation statistique, un lien.
Format des resultats donnés par scipyR
from scipy.stats import linregress
linregress(df['petal length (cm)'], df['petal width (cm)'])regression <- lm(iris$Petal.Length~iris$Petal.Width)
summary(regression)LinregressResult(
slope=0.41575541635241114, intercept=-0.36307552131902776,
rvalue=0.9628654314027963, pvalue=4.6750039073255014e-86,
stderr=0.009582435790766206, intercept_stderr=0.03976198987309611
)##
## Call:
## lm(formula = iris$Petal.Length ~ iris$Petal.Width)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.33542 -0.30347 -0.02955 0.25776 1.39453
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.08356 0.07297 14.85 <2e-16 ***
## iris$Petal.Width 2.22994 0.05140 43.39 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4782 on 148 degrees of freedom
## Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266
## F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16Coefficients du modèle ajusté, R (et non R²), la p-value, écart-type des erreurs sur les coefficients.
Distribution des résidus, coefficients du modèle ajusté et leur p-value associée (ici sur un test de Student, notée Pr(>|t|) et R2)
Bonus: Critères de significativité du lien linéaire
Les résidus $\epsilon_i$ (écart entre valeur observée et valeur prédite $(V_2−\hat{V}_2)$ par le modèle pour l’individu i) doivent:
- être indépendants : covariance nulle ou très faible
$cov(x_i,\epsilon_i)=0$ - être distribués selon un loi normale de moyenne nulle
$\epsilon \sim \mathcal{N}(0,\sigma_{\epsilon})$ - être distribués de façon homogène (homoscédasticité), i.e. de variance constante $var(\epsilon_i)=\sigma^2_\epsilon$ , indépendante de l’observation.
Bonus : évaluation de l'indépendance des résidus avec statsmodelsR
Graphique de la fonction plot_acf :
Si une barre (exceptée la première) dépasse la zone bleutée, on peut remettre en cause l’indépendance des résidus. Ici, c’est le cas.
Graphique de la fonction acf :
Si une barre (exceptée la première) dépasse la ligne en pointillés, on peut remettre en cause l’indépendance des résidus. Ici, c’est le cas.
import statsmodels.api as sm
import matplotlib.pyplot as plt
reg = linregress(df['petal length (cm)'], df['petal width (cm)'])
residuals = df['petal width (cm)'] - ( reg.intercept + reg.slope * df['petal length (cm)'] )
sm.graphics.tsa.plot_acf(residuals, lags=20)
plt.show()modele1 <- lm(iris$Petal.Length~ iris$Petal.Width)
acf(residuals(modele1))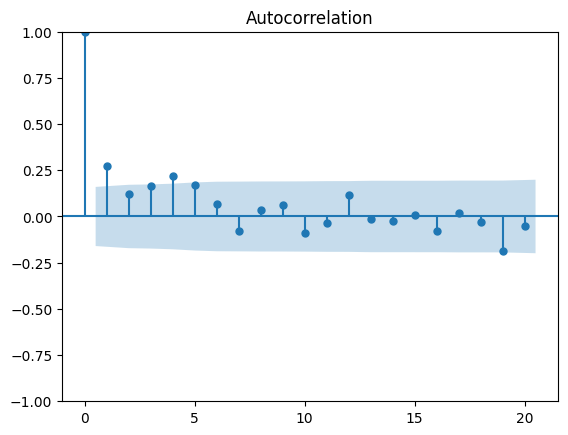
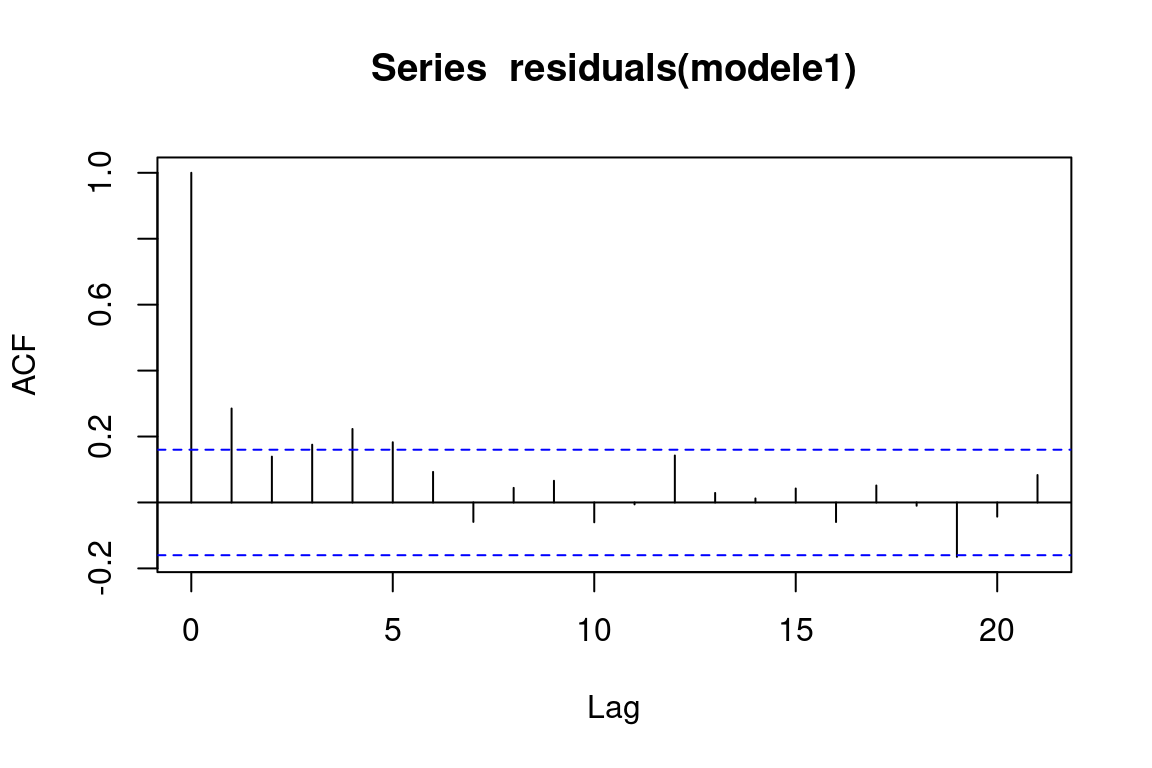
Bonus : Évaluer l’homogénéité des résidus avec statsmodelsR
Graphique de la fonction plot_acf :
Si une barre (exceptée la première) dépasse la zone bleutée, on peut remettre en cause l’indépendance des résidus. Ici, c’est le cas.
Graphique de la fonction acf :
Si une barre (exceptée la première) dépasse la ligne en pointillés, on peut remettre en cause l’indépendance des résidus. Ici, c’est le cas.
import statsmodels.api as sm
import matplotlib.pyplot as plt
reg = linregress(df['petal length (cm)'], df['petal width (cm)'])
residuals = df['petal width (cm)'] - ( reg.intercept + reg.slope * df['petal length (cm)'] )
sm.graphics.tsa.plot_acf(residuals, lags=20)
plt.show()modele1 <- lm(iris$Petal.Length~ iris$Petal.Width)
acf(residuals(modele1))

Corrélation de deux variables quantitatives
Corrélation (linéaire)
Dans le cas d’une liaison statistique linéaire entre deux variables, on peut calculer l’«intensité» de ce lien sans nécessairement trouver les coefficients modèle linéaire : c’est la corrélation
$cor(x, y) \in [-1; 1]$ entre deux variables $x$ et $y$
- +1 : les deux variables croissent ou décroissent conjointement
- -1 : quand l’une des variables croît, l’autre décroît.
- 0 : pas de relation linéaire entre les deux variables
Calcul direct du coefficient de corrélation (de Pearson)
Soient deux variables $V_1$ et $V_2$
Le coefficient de corrélation $r$ de $V_1$ et $V_2$ est la normalisation de la covariance par le produit des écart-types des variables
$r = \frac{cov(V_1, V_2)}{\sigma_{V_1}\sigma_{V_2}}$
La covariance est la moyenne du produit des écarts à la moyenne
$cov(V1,V2)=\mathbb{E}[(V1−\mathbb{E}[V1])(V2−\mathbb{E}[V2])]$
Test de corrélation entre deux variables avec scipyR
Version plus complète : c’est un test, on a plusieurs indicateurs statistiques sur ce test, notamment la p-value et l’intervalle de confiance
from scipy.stats import pearsonr
result = pearsonr(df['petal length (cm)'], df['petal width (cm)'])
print(result, result.confidence_interval(0.95))cor.test(iris$Petal.Length, iris$Petal.Width)PearsonRResult(statistic=0.962865431402796, pvalue=4.675003907328653e-86)
ConfidenceInterval(low=0.9490524593111143, high=0.972985317378797)##
## Pearson's product-moment correlation
##
## data: iris$Petal.Length and iris$Petal.Width
## t = 43.387, df = 148, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.9490525 0.9729853
## sample estimates:
## cor
## 0.9628654Rappel : la p-value quantifie la significativité du test. En général, on considère le test significatif si elle est en dessous de 5%, soit 0.05.
Test de corrélation entre deux variables avec scipyR
df.corr(method='pearson')cor(iris[,1:4])| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| sepal length (cm) | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal width (cm) | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal length (cm) | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal width (cm) | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
## Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
## Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
## Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000
Présentation des corrélations entre les variables quantitatives d’un tableau, pour tous les couples de variables.
La matrice de corrélation est symétrique, et sa diagonale est constituée de 1.
Sensibilité aux outliers
X = [3,2,3,4,1,2,3,4,5,2,3,4,3]
Y = [1,2,2,2,3,3,3,3,3,4,4,4,5]
plt.figure(figsize=(16, 6))
plt.plot(X, Y, 'o')
plt.xlim(0, 16)
plt.ylim(0, 16)
plt.show()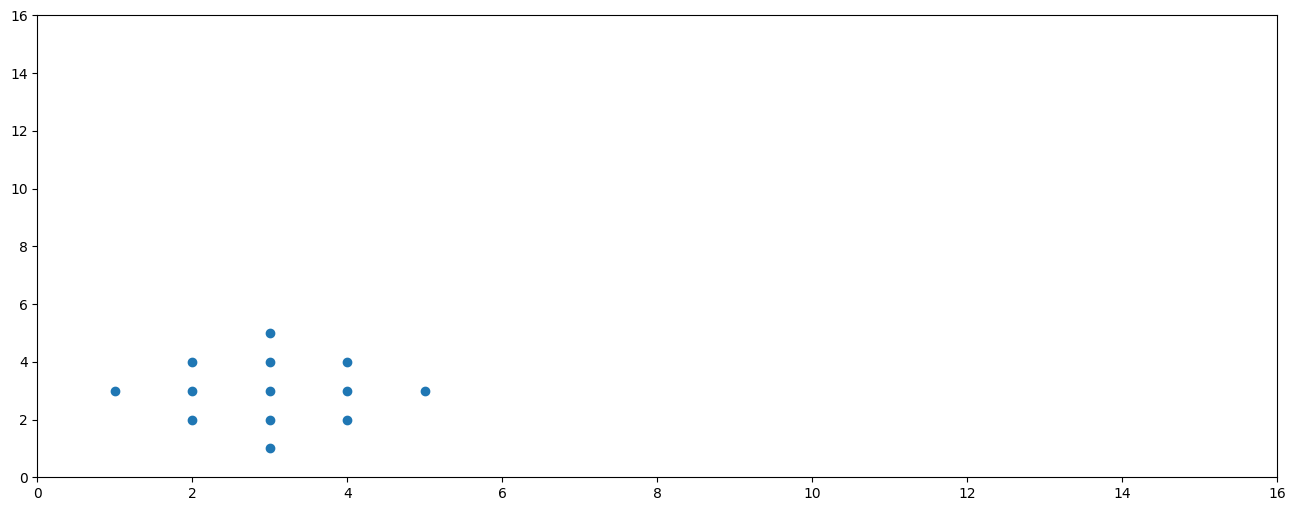
pearsonr(X, Y).statistic0.00Sensibilité aux outliers
X = [3,2,3,4,1,2,3,4,5,2,3,4,3, 15]
Y = [1,2,2,2,3,3,3,3,3,4,4,4,5, 15]
plt.figure(figsize=(16, 6))
plt.plot(X, Y, 'o')
plt.xlim(0, 16)
plt.ylim(0, 16)
plt.show()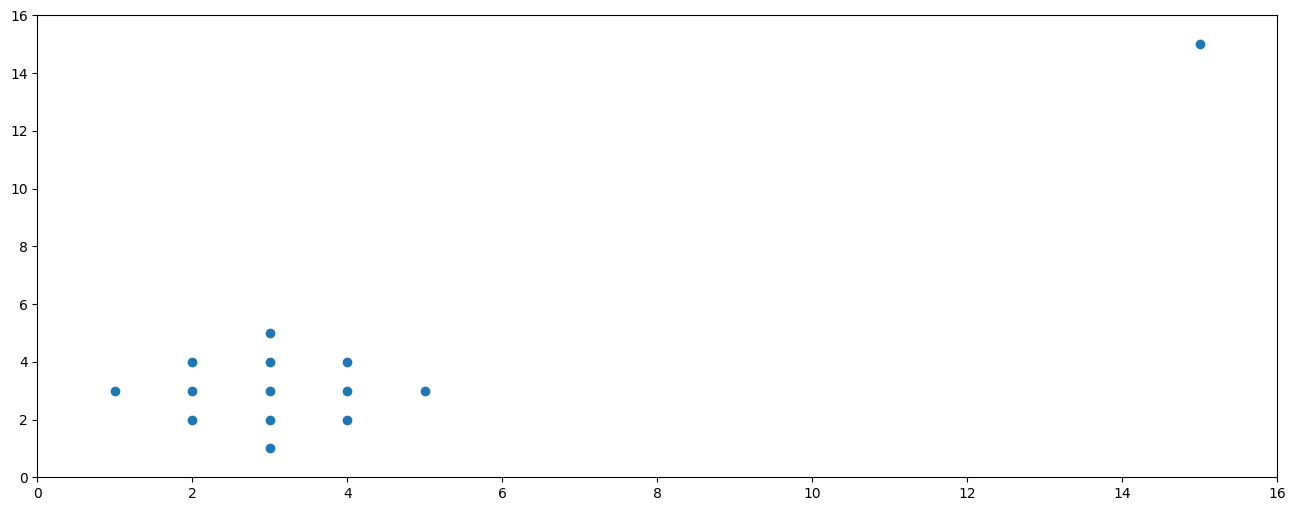
pearsonr(X, Y).statistic0.9052224371373307Sensibilité aux outliers
Outlier : observation “anormale”, par sa valeur extrême, comparée aux autres
La corrélation et la régression linéaire sont très sensibles aux outliers.
→ s’interroger sur la nécessité de nettoyer/filtrer les données et des conséquences
Que faire lorsque la relation n’est pas linéaire ?
Quand les deux variables semblent corrélées, de façon monotone mais non linéaire,
→ Coefficient de Spearman, basé sur le rang des individus.
$\rho = 1 - \frac{6\Sigma_{i=1}^n (rg(X_i) - rg(Y_i) )^2 }{n^3 - n}$
avec :
$rg(X_i)$ le rang de $X_i$ (le classement de sa valeur) dans la distribution de $X$
$n$ le nombre d'individus
Obtenir le coefficient de Spearman avec scipyR
from scipy.stats import spearmanr
spearmanr(df['sepal length (cm)'], df['sepal width (cm)'])cor.test(iris$Sepal.Length, iris$Sepal.Width, method="spearman", exact = FALSE)SignificanceResult(statistic=-0.166777658283235, pvalue=0.04136799424884587)##
## Spearman's rank correlation rho
##
## data: iris$Sepal.Length and iris$Sepal.Width
## S = 656283, p-value = 0.04137
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## -0.1667777l’argument exact doit être précisé en cas de valeurs ex aequo dans les données.
Utilisation conjointe des coefficients de Pearson et Spearman
$r$ (Pearson) et $\rho$ (Spearman) sont deux moyens d'estimer la corrélation, lequel choisir ?
si $r=\rho$ : on garde r (plus simple à interpréter)
si $|r|<|\rho|$ : la relation est non-linéaire : prendre $\rho$
si $|r|>|\rho|$ : il y a un biais, prendre $\rho$ (plus robuste)
… et toujours tracer le nuage de points pour examiner la nature de la relation.
“trucs” pour linéariser des relations non-linéaires
Relation log-linéaire
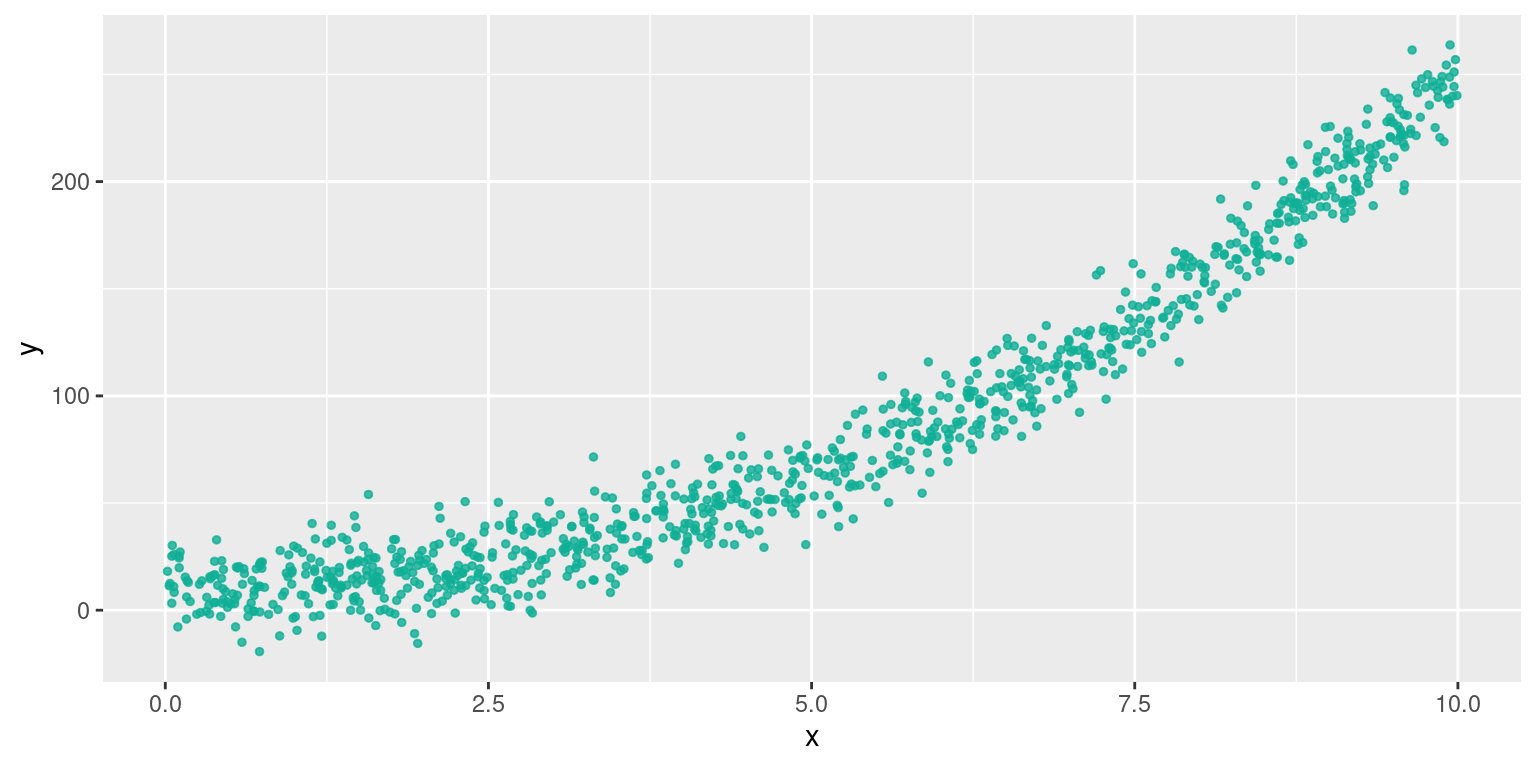
Relation de $y = ax^b$
Se linéarise par $ln(y) = b\times ln(x)+ln(a)$
Relation géométrique (exponentielle)
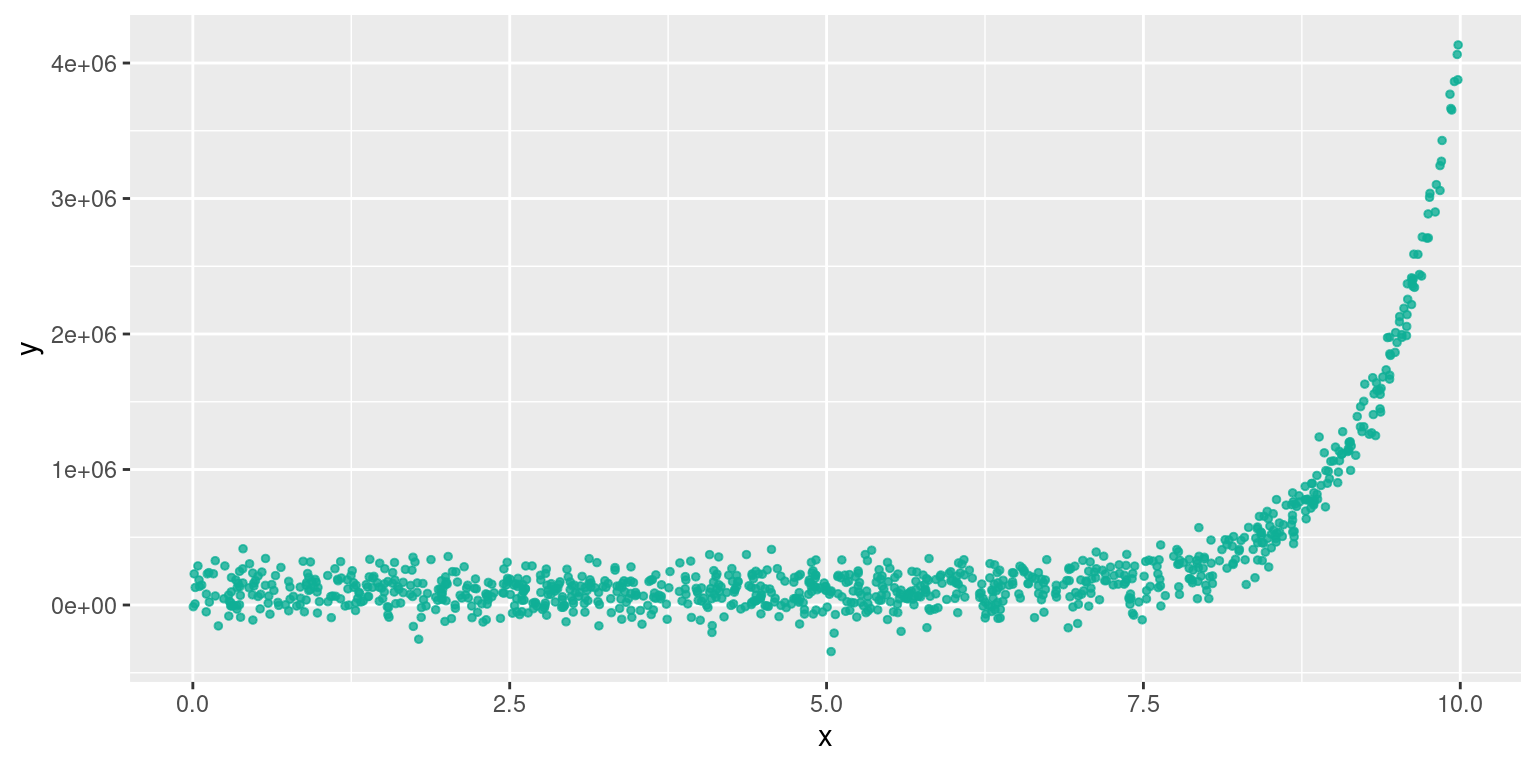
Relation de $y = e^{ax+b}$
Se linéarise par $ln(y) = ax+ln(b)$
Relation logarithmique
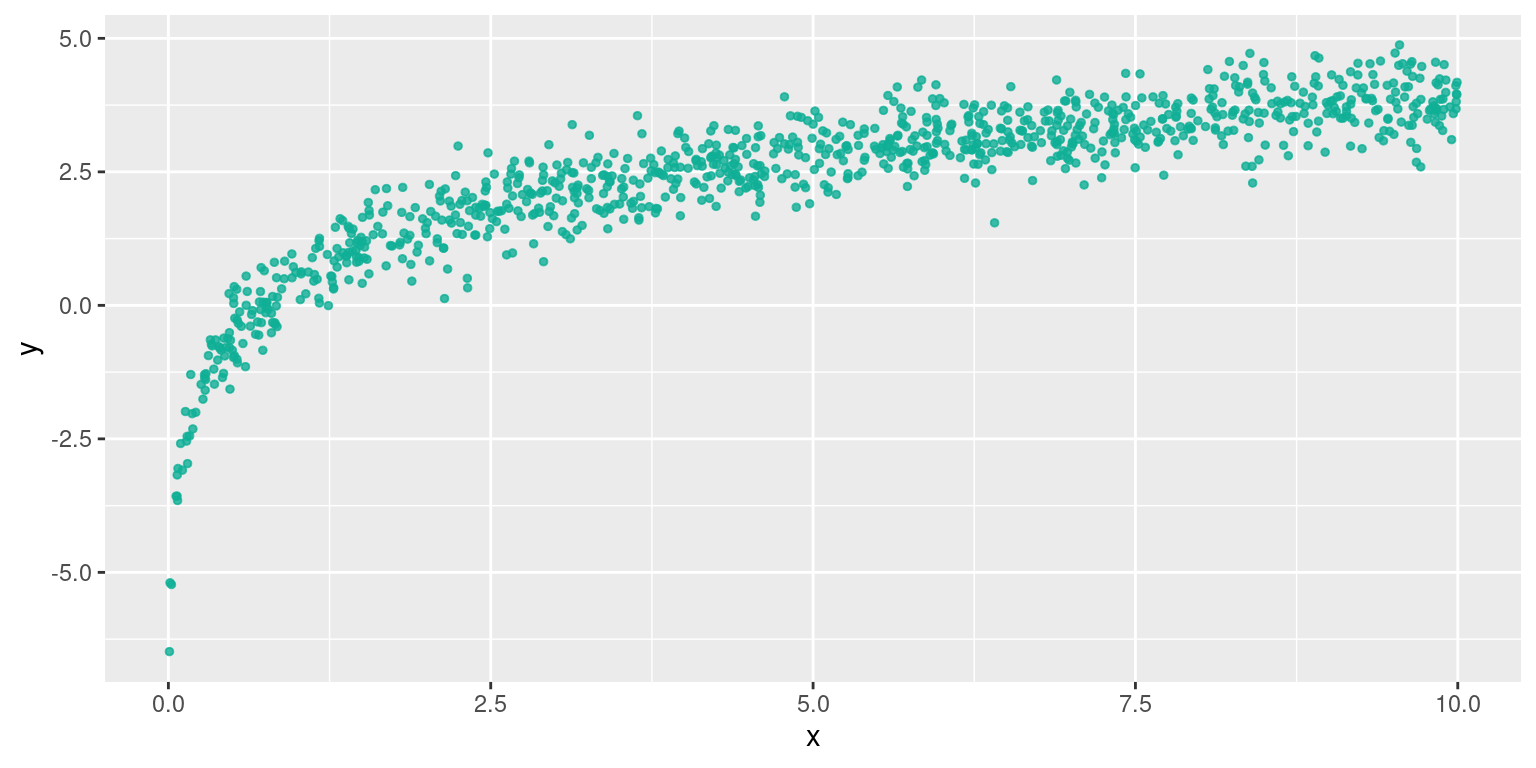
Relation de $y = a \times ln(x)+b$
→ changement de variable
Relation logistique
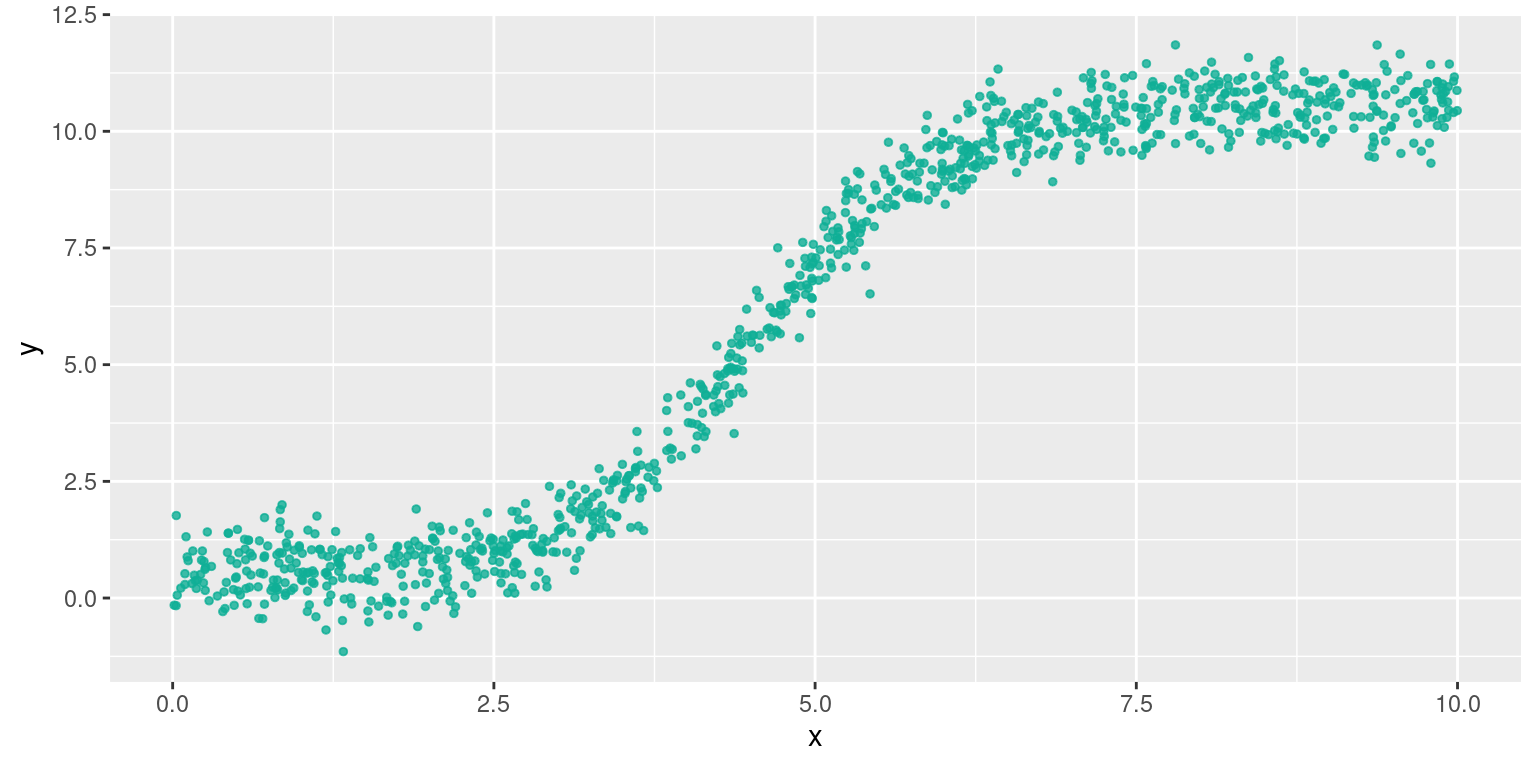
Relation de $y = y_{min} + \frac{y_{max} - y_{min}}{1 + e^{ax+b}}$
Se linéarise par $ln(\frac{y_{max} - y}{y - y_{min}}) = ax+b$
Liens entre deux variables qualitatives
Représentation graphique
Pour deux variables qualitatives, on ne peut pas produire de nuages de points, ni de droites de régression.
→ On peut représenter la table de contingence (cf fonctions statsmodels.graphics.mosaicplot.mosaic et pandas.crosstab)

Test statistique dit du “Chi 2” ou “Chi carré”
Le test du $\chi^2$ est un test d’indépendance, il mesure l’écart, la différence, entre deux distributions de variables qualitatives.
Il répond à la question : “Existe-t-il un lien statistique entre deux séries de valeurs qualitatives”
(La réponse est de type OUI/NON , le $\chi^2$ ne donne pas l’intensité du lien)
Test statistique dit du “Chi 2” ou “Chi carré”
- Hypothèse nulle $H_0$ : les deux distributions sont indépendantes.
- «Faire le test» permet de conserver ou de rejeter cette hypothèse
Principe du Chi 2
- On génère une population théorique à laquelle on va comparer la population observée en considérant leurs distributions.
- Cette distribution théorique reflête ce qui se passerait si on suppose que $H_0$ est vraie.
- Avec cette comparaison, on pourra conserver ou de rejeter l'hypothèse nulle.
La création de cette distribution se fait à partir du tableau de contingence.
Tableau de contingence
C'est un tableau à double entrée qui croise deux variables qualitatives.
Dans une case on trouve l’effectif (= le nombre) des individus caractérisés par la conjonction des modalités en ligne et en colonnes.
Exemple sur des formes géométriques de couleurs :
| blanc | noir | |
|---|---|---|
| carré | 22 | 12 |
| rond | 10 | 30 |
| triangle | 26 | 5 |
Avec pandas : fonction crosstab
En R : fonction table()
Construction de la distribution théorique
On commence par sommer les effectifs selon les modalités (en ligne et en colonne)
| blanc | noir | total | |
|---|---|---|---|
| carré | 22 | 12 | 34 |
| rond | 10 | 30 | 40 |
| triangle | 26 | 5 | 31 |
| total | 58 | 47 | 105 |
On appelle les sommes en lignes et en colonnes sommes marginales, elles sont mises dans les “marges” du tableau.
Construction de la distribution théorique
En divisant par la taille de la population, on obtient les fréquences observées
| blanc | noir | total | |
|---|---|---|---|
| carré | 0.20952381 | 0.11428571 | 0.3238095 |
| rond | 0.09523810 | 0.28571429 | 0.3809524 |
| triangle | 0.24761905 | 0.04761905 | 0.2952381 |
| total | 0.552381 | 0.447619 | 1 |
On obtient les pourcentages de l’effectif dans les cases du tableau.
C’est également la probabilité qu’un individu de la population observée soit caractérisé par les modalités en ligne et en colonne.
Construction de la distribution théorique
| blanc | noir | total | |
|---|---|---|---|
| carré | 0.20952381 | 0.11428571 | 0.3238095 |
| rond | 0.09523810 | 0.28571429 | 0.3809524 |
| triangle | 0.24761905 | 0.04761905 | 0.2952381 |
| total | 0.552381 | 0.447619 | 1 |
De la même façon, les fréquences marginales (marges divisées par la taille de la pop.), donnent la probabilité d’observer un individu de la modalité correspondant à la ligne ou à la colonne considérée.
Exemple : dans cette population , j’ai 29.5% de chances de tirer un triangle, et 55% de chances de tirer une pièce blanche.
Construction de la distribution théorique
Rappel : probabilité conjointe de deux événements indépendants :
$P(A \cap B) = P(A) \times P(B)$
À partir des fréquences marginales précédentes, on obtient pour chaque couple de modalités, la probabilité théorique, celle qui suppose $H_0$, par un simple produit.
Exemple : Si $H_0$ est vraie, la probabilité d’observer un triangle noir est donnée par:
$P(triangle∩noir)=P(triangle)×P(noir)$
$P(triangle∩noir)=0.447619×0.2952381=0.1321542$
La probabilité théorique d’observer un triangle noir est de 13,2%
Construction de la distribution théorique
On crée un second tableau, dont chaque case vaut le produit des fréquences marginales calculées sur le tableau des observations.
| blanc | noir | total | |
|---|---|---|---|
| carré | 0.1788662 | 0.1449433 | 0.3238095 |
| rond | 0.2104309 | 0.1705215 | 0.3809524 |
| triangle | 0.1630839 | 0.1321542 | 0.2952381 |
| total | 0.552381 | 0.447619 | 1 |
C'est le tableau des fréquences théoriques.
Tableau des effectifs théoriques
On l’obtient en multipliant les fréquences théoriques par la taille de la population observée (ici 105)
| blanc | noir | |
|---|---|---|
| carré | 18.78095 | 15.21905 |
| rond | 22.09524 | 17.90476 |
| triangle | 17.12381 | 13.87619 |
N.B. Il n’est pas nécessaire d’arrondir les effectifs théoriques.
Calcul du Chi 2
C’est la somme, pour chaque case du tableau de contingence (i.e. pour chaque couple de modalités), des écarts carrés entre effectif observé et effectif théorique, divisés par l’effectif théorique.
Soient $T^{obs}$ le tableau des effectifs observés, $T^{theo}$ le tableau des effectifs théoriques,
$\chi^2 = \sum_{i, j}\frac{(T^{obs}_{i,j}−T^{theo}_{i,j})^2}{T^{theo}_{i,j}}$
Ici : $\chi^2=26.30329$
Interprétation du Chi 2
Il faut comparer la valeur du $\chi^2$ calculée avec la valeur critique qu’on trouve dans une table de loi du chi 2.
C’est un tableau à double entrée : une valeur de quantile, et un degré de liberté.
On peut considérer que la valeur de quantile est le pourcentage d’erreur qu’on s’autorise de faire. On prend souvent 5% : la colonne 1-0.05 = 0.95
Le degré de liberté est obtenu en calculant la valeur :
$(nb_{lignes}−1)∗(nb_{colonnes}−1)$.
Dans notre exemple , le degré de liberté est 2*1 = 2
Table de loi du Chi 2
Si $X$ suit une loi du $\chi^2$ de degré d, la valeur critique v est telle que :
$P(X < v)=1-\alpha$
| $d \downarrow \alpha \rightarrow$ | 0.95 | 0.9 | 0.8 | 0.7 | 0.5 | 0.3 | 0.2 | 0.1 | 0.05 | 0.01 | 0.001 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.003932 | 0.015791 | 0.064185 | 0.148472 | 0.454936 | 1.074194 | 1.642374 | 2.705543 | 3.841459 | 6.634897 | 10.827566 |
| 2 | 0.102587 | 0.210721 | 0.446287 | 0.713350 | 1.386294 | 2.407946 | 3.218876 | 4.605170 | 5.991465 | 9.210340 | 13.815511 |
| 3 | 0.351846 | 0.584374 | 1.005174 | 1.423652 | 2.365974 | 3.664871 | 4.641628 | 6.251389 | 7.814728 | 11.344867 | 16.266236 |
| 4 | 0.710723 | 1.063623 | 1.648777 | 2.194698 | 3.356694 | 4.878433 | 5.988617 | 7.779440 | 9.487729 | 13.276704 | 18.466827 |
| 5 | 1.145476 | 1.610308 | 2.342534 | 2.999908 | 4.351460 | 6.064430 | 7.289276 | 9.236357 | 11.070498 | 15.086272 | 20.515006 |
| 6 | 1.635383 | 2.204131 | 3.070088 | 3.827552 | 5.348121 | 7.231135 | 8.558060 | 10.644641 | 12.591587 | 16.811894 | 22.457744 |
| 7 | 2.167350 | 2.833107 | 3.822322 | 4.671330 | 6.345811 | 8.383431 | 9.803250 | 12.017037 | 14.067140 | 18.475307 | 24.321886 |
| 8 | 2.732637 | 3.489539 | 4.593574 | 5.527422 | 7.344121 | 9.524458 | 11.030091 | 13.361566 | 15.507313 | 20.090235 | 26.124482 |
| 9 | 3.325113 | 4.168159 | 5.380053 | 6.393306 | 8.342833 | 10.656372 | 12.242145 | 14.683657 | 16.918978 | 21.665994 | 27.877165 |
| 10 | 3.940299 | 4.865182 | 6.179079 | 7.267218 | 9.341818 | 11.780723 | 13.441958 | 15.987179 | 18.307038 | 23.209251 | 29.588298 |
| 11 | 4.574813 | 5.577785 | 6.988674 | 8.147868 | 10.340998 | 12.898668 | 14.631421 | 17.275009 | 19.675138 | 24.724970 | 31.264134 |
| 12 | 5.226029 | 6.303796 | 7.807328 | 9.034277 | 11.340322 | 14.011100 | 15.811986 | 18.549348 | 21.026070 | 26.216967 | 32.909490 |
| 13 | 5.891864 | 7.041505 | 8.633861 | 9.925682 | 12.339756 | 15.118722 | 16.984797 | 19.811929 | 22.362032 | 27.688250 | 34.528179 |
| 14 | 6.570631 | 7.789534 | 9.467328 | 10.821478 | 13.339274 | 16.222099 | 18.150771 | 21.064144 | 23.684791 | 29.141238 | 36.123274 |
Interprétation du Chi 2
D’après le tableau de la loi du $\chi^2$, la valeur critique pour un test avec 5% de chances de se tromper est un degré de liberté de 2 vaut 5.991.
Si la valeur calculée du $\chi^2$ est supérieure à la valeur critique, on rejette $H_0$
Pour notre exemple: On rejette $H_0$, i.e. les deux variables sont dépendantes, car $\chi^2≈26>5.991$
Interprétation: «la forme est liée à la couleur dans cette population, nous pouvons l’affirmer avec un risque d’erreur d’au moins 5%»
Les étapes du Chi 2
- Tableau de contingence
- Sommes marginales
- Calcul des fréquences observées
- Calcul des fréquences théoriques
- Tableau d’effectifs théoriques
- Calcul de la valeur du test
- Comparaison avec les valeurs de la table de Chi 2
Bonus : Information Mutuelle
- Quantifie la dépendance statistique entre les variables.
- Basée sur la théorie de l'information de Shannon.
- A partir du tableau des fréquences observées.
$I(X; Y) = \sum_{x, y}P(X=x, Y=y) log_2 \frac{P(X=x, Y=y)}{P(X=x)P(X=y)}$
- $I(X; Y) = 0 \Leftrightarrow$ X et Y sont indépendants.
- Plus I est grand, plus la dépendance entre les variables est importante.
Exemple
Soient deux variables X et Y suivant une loi uniforme sur {"pile", "face"}, et complétement dépendantes (X=Y).
On construit la table des fréquences observées :
| pile | face | total | |
|---|---|---|---|
| pile | 0.5 | 0 | 0.5 |
| face | 0 | 0.5 | 0.5 |
| total | 0.5 | 0.5 | 1 |
$I(X; Y) = 0.5\times log_2\frac{0.5}{0.5 \times 0.5} + 0 + 0.5\times log_2\frac{0.5}{0.5 \times 0.5} + 0$
$I(X; Y) = 0.5\times log_2(2) + 0.5\times log_2(2)$
$I(X; Y) = log_2(2) = 1$
Que se serait-il passé si X et Y avaient été uniformes sur n modalités ?
Exemple
Soient deux variables X et Y suivant une loi uniforme sur {"pile", "face"}, et complétement indépendantes.
On construit la table des fréquences observées :
| pile | face | total | |
|---|---|---|---|
| pile | 0.25 | 0.25 | 0.5 |
| face | 0.25 | 0.25 | 0.5 |
| total | 0.5 | 0.5 | 1 |
$I(X; Y) = 4 \times (0.25\times log_2\frac{0.25}{0.5 \times 0.5})$
$I(X; Y) = 1\times log_2(1)$
$I(X; Y) = 0$
Lien entre une variable qualitative et une variable quantitative.
Représentation graphique
Pas de moyen simple de calculer le lien entre une variable qualitative et une variable quantitative.
- corrélation de rang
- régression logistique
- analyse de la variance (ANOVA)
⟹ Alors on fait un graphique !
La variable qualitative sert de catégorie, on fait varier la représentation graphique de la variable quantitative suivant cette catégorie.
2 possibilités :
- boîtes à moustaches
- superposition d’histogrammes / densités
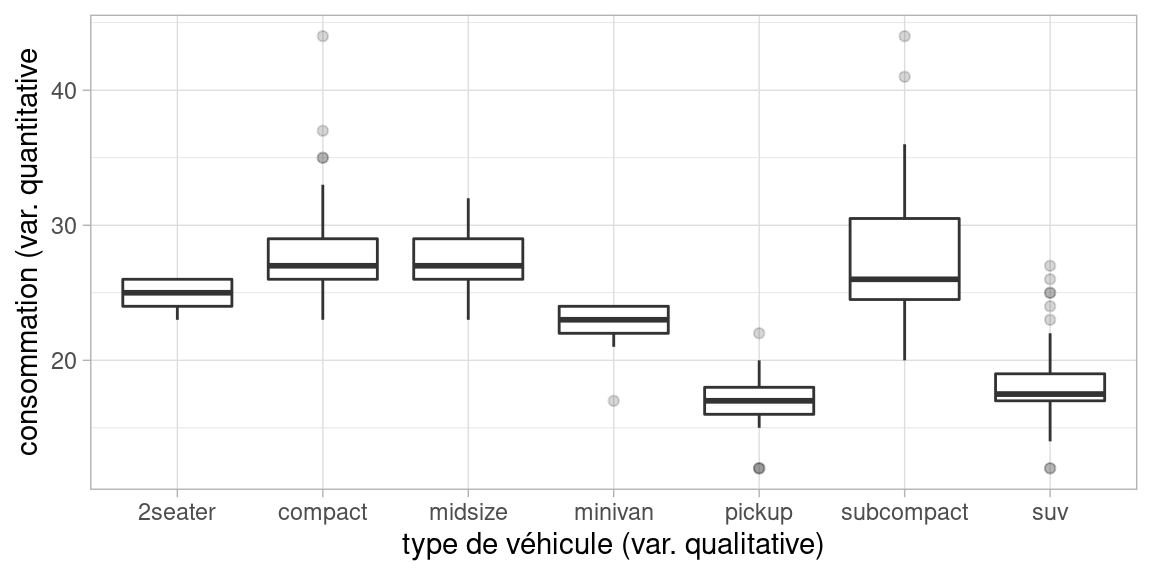
Boxplot par catégories
Principe : on trace un boxplot par modalité de la variable qualitative
E.g. : consommation de véhicules par type (dataset mpg de R)
Bonus : ANOVA (Analyse de la Variance)
Test pour vérifier si les moyennes de la variable quantitative pour les différentes modalités de la variable qualitative sont significativement différentes.
- Hypothèse nulle (H0) : Toutes les moyennes des groupes sont égales.
- Hypothèse alternative (Ha) : Au moins une moyenne est différente.
- On compare la variance entre les groupes à la variance à l'intérieur des groupes.
$V_{inter-groupes} = \frac{1}{p-1}\sum_{i=1}^p n_i(\bar{x_i}-\bar{x})^2$
$V_{intra-groupes} = \frac{1}{N-p}\sum_{i=1}^p \sum_{j=1}^{n_i} (x_i^j-\bar{x_i})^2$
Avec $p$ le nombre de groupes, $N$ le nombre d'individu, $\bar{x}$ la moyenne de toute la population, $\bar{x_i}$ la moyenne du groupe i, $n_i$ le nombre d'individu du groupe i et $x_i^j$ le $j^e$ individu du groupe i.
On calcule le rapport $F = \frac{\text{Variance entre les groupes}}{\text{Variance intra-groupe}}$
Bonus : ANOVA (Analyse de la Variance)
- Si (H0), F est faible.
- Si les moyennes des groupes sont très différentes de la moyenne de la population, F augmente.
- Si les groupes ont une grande dispersion, F dimiminue.
Si (H0), F suit une loi de Fischer de degrés (p-1, N-p).
La p-value est la probabilité qu'une loi de Fischer de degrés (p-1, N-p) ait une valeur $\geq$ F. Si la p-value est faible ($<$0.05), on peut rejeter (H0).
⚠Limite du test : pour que l'ANOVA ait un sens, il faut que les populations de chaque groupe (1) suivent une loi normale et (2) aient la même variance⚠