Analyse Multivariée
M2 IGAST
Martin Cubaud
LASTIG-UGE-IGN/ENSG
2025-2026

Plan du cours
Ce cours est construit à partir du cours M2 IGAST 2022 d'Ana-Maria Olteanu-Raimond.
- Introduction et rappels
- Analyse factorielle
- ACP
- Cercle des corrélations
- Classification
- Non-supervisée
- Supervisée
Introduction et rappels
Analyse multivariée - principes
Analyse multivariée = les données sont multidimensionnelles.
| gid | nom | Code insee | Alt_moy | Pente_moy | De_relig | ... |
|---|---|---|---|---|---|---|
| 1 | RENCUREL | 38333 | 1114 | 74 | 0,02893089 | |
| 2 | MALLEVAL-EN-VERCORS | 38216 | 1114 | 74 | 0,07057872 | |
| 3 | MURIANETTE | 38271 | 1027 | 73 | 0 | |
| 4 | CHAMP-SUR-DRAC | 38071 | 215 | 2 | 0,4742854 | |
| 5 | JARRIE | 38200 | 385$X_{ij}$ | 46 | 0,22279623 | |
| 6 | AUTRANS | 38021 | 1305 | 42 | 0,02277919 | |
| 7 | MONTCHABOUD | 38252 | 518 | 71 | 0,50559645 | |
| 8 | PONT-EN-ROYANS | 38319 | 409 | 43 | 0 |
Quelles sont les communes qui se ressemblent ? Quelles sont les variables qui permettent d'identifier les ressemblances / dissemblances ?
Analyse Multi-Variée - Principes
A chaque individu (unité spatiale), on associe son vecteur $X_i$, contenant la $i^{ème}$ ligne :
$X_i = (X_{i,1} ... X_{i,M})$
A chaque variable, on associe son vecteur $V_j$, contenant la $j^{ème}$ colonne :
$V_j = \begin{pmatrix}X_{1,j}\\...\\X_{N,j}\end{pmatrix} \rightarrow$ Moyenne, écart-type, variance
Distances entre unités spatiales
Pas une distance géographique, mais une distance prenant en compte les valeurs des variables.
Deux individus sont proches dans "l'espace des distances" si la distance est faible.
Il existe plusieurs distances : euclidienne, Manhattan...
⚠ Normaliser les variables avant de calculer une distance !
⚠ Variables qualitatives : Encodage, distances sur les hierarchies...
Distances entre unités spatiales
Distance euclidienne
$d(i_1,i_2)=\sqrt{\sum_{j=1}^M(X_{i_1,j} - X_{i_2, j})^2}$
Distance euclidienne au carré : Permet de renforcer l’effet des distances entre les objets éloignés (atypiques)
Distance de Manhattan
$d_M(i_1,i_2)=\sum_{j=1}^M|X_{i_1,j} - X_{i_2, j}|$
"Distance" cosinus : ignore la magnitude, plus stable en haute dimension
$d_{cos}(i_1, i_2)=1 - \frac{\sum_{j=1}^M X_{i_1,j} X_{i_2, j}}{\sqrt{\sum_{j=1}^M X_{i_1,j}^2} \sqrt{\sum_{j=1}^M X_{i_2,j}^2}}$

(wikipedia)
Distance de Manhattan vs Euclidienne
E.g. pour 2 variables $x$ et $y$, en notant $\Delta x = x_2 - x_1$ et $\Delta y = y_2 - y_1$ :
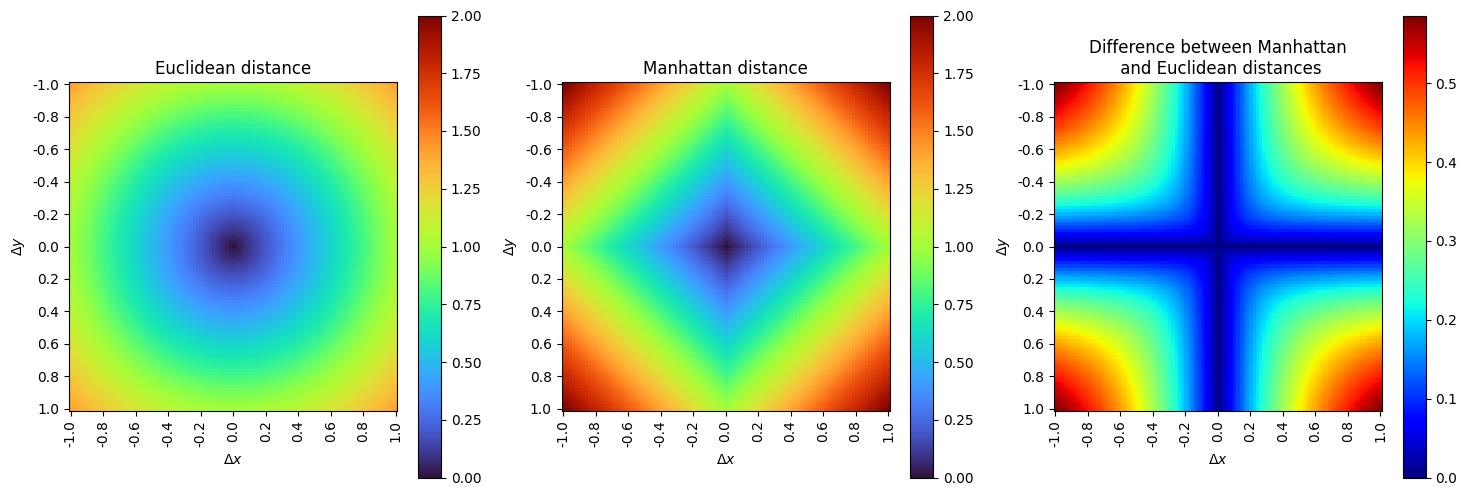
- La distance de Manhattan est toujours supérieure ou égale à celle Euclidienne.
- La différence est plus importante lorsque les 2 variables varient en même temps.
- Si une des variables est fixée, augmenter la distance sur l'autre variable fait augmenter la différence.
étape préalable : Centrer-réduire
Centrer permet de mettre l'origine du système d'axes au centre de gravité du nuage de points; $G$ = vecteur des moyennes arithmétiques de chaque variable.
$G = \begin{pmatrix}\bar{V_{1}}\\...\\\bar{V_{M}}\end{pmatrix}, \bar{V_j}=\frac{1}{N}\sum_{i=1}^N X_{i,j}$
Matrice centrée :
$X_c = \begin{pmatrix} X_{1,1} - \bar{V_{1}} &... &X_{1,M} - \bar{V_{M}}\\ \vdots &\ddots& \vdots \\ X_{N,1} - \bar{V_{1}} &... &X_{N,M} - \bar{V_{M}}\end{pmatrix}$
étape préalable : Centrer-réduire
Réduire permet de rendre comparables les variables exprimées sur des échelles (unités) différentes.
écart-type $\sigma_j = \sqrt{ \frac{1}{N} \sum_{i=1}^N (X_{i,j} - \bar{V_j})^2 }$
Matrice centrée réduite :
$X_{cr} = \begin{pmatrix} \frac{X_{1,1} - \bar{V_{1}}}{\sigma_1} &... & \frac{X_{1,M} - \bar{V_{M}}}{\sigma_M}\\ \vdots &\ddots& \vdots \\ \frac{X_{N,1} - \bar{V_{1}}}{\sigma_1} &... &\frac{X_{N,M} - \bar{V_{M}}}{\sigma_M}\end{pmatrix}$
Analyse Factorielle
Analyse en composantes principales
Objectifs de l'ACP :
- Permet de résumer un grand nombre de variables en 2-3 dimensions.
- Fournit des nouvelles variables, composantes principales, non corrélées entre elles.
- Décrire et visualiser le lien entre les données.
- Réduire le nombre de dimensions = de variables à utiliser.
- Utile pour la classification : gain de temps, gain de stabilité, facilite l'interprétation...
- Débruiter les données.
Exemple en 2D
On a 2 variables X et Y assez corrélées.
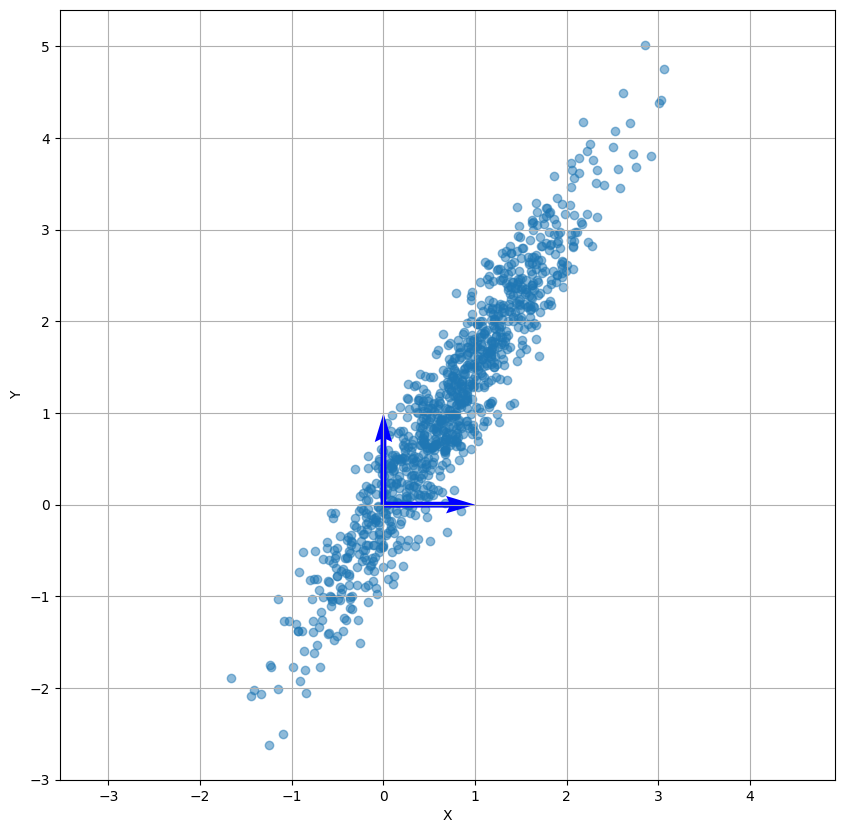
On veut résumer l'information en une seule variable.
Exemple en 2D
Etape 1 : centrer-réduire
$X_{cr} = \frac{X - \bar{X}}{\sigma_X}, Y_{cr} = \frac{Y - \bar{Y}}{\sigma_Y}$
Exemple en 2D
Etape 2 : calcul de la matrice de corrélation
Matrice de la corrélation entre chaque paire de variable. Si on a M variables, la matrice est de taille M$\times$M.
$cor(X, Y)=cov(X_{cr}, Y_{cr})=\frac{1}{N}\sum_{i=1}^N X_{cr_i}Y_{cr_i}$
$COR = \begin{pmatrix} cor(X, X) & cor(X, Y) \\ cor(Y, X) & cor(Y, Y) \end{pmatrix} = \begin{pmatrix} 1 & 0.89 \\ 0.89 & 1 \end{pmatrix}$
Exemple en 2D
Etape 3 : chercher les directions de plus grande variance = Les vecteurs propres.
On cherche ces directions comme combinaisons linaires des anciennes variables.
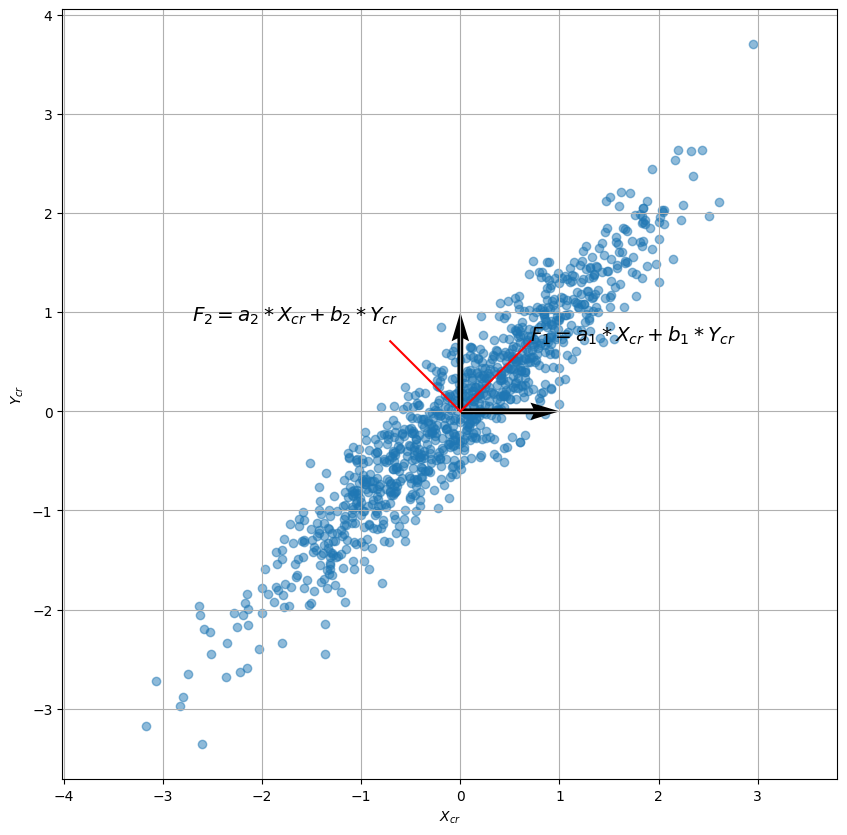
Exemple en 2D
On cherche $F_1 = a X_{cr} + b Y_{cr}$ qui maximise $var(F_1)$. (Avec $a^2+b^2=1$)
$var(F_1)=var(a X_{cr} + b Y_{cr}) = a^2 var(X_cr) + b^2 var(Y_cr) + 2ab Cov(X_cr, Y_cr)$
$var(F_1)=\begin{pmatrix} a & b \end{pmatrix} COR \begin{pmatrix} a \\ b \end{pmatrix} \rightarrow$ Maximal si $ COR \begin{pmatrix} a \\ b \end{pmatrix}$ est dans la même direction que $\begin{pmatrix} a \\ b \end{pmatrix}.$
Exemple en 2D
Les vecteurs propres $\vec{v_1},...,\vec{v_M}$ sont des vecteurs unitaires tels que $COR\vec{v_j} = \lambda_j\vec{v_j}$
Les $\lambda_j$ sont appelés les valeurs propres. $\lambda_j$ est la variance expliquée par le vecteur propre j.
$\rightarrow$ Calculer les valeurs propres : solutions $\lambda$ de $DET(COR - \lambda Id) = 0$.
$\rightarrow$ Calculer le vecteur propre associé à $\lambda_j$ : solution $\vec{v}$ de $(COR - \lambda_j Id)\vec{v} = \vec{0}$.
Exemple en 2D
Etape 4 : Construire les nouvelles variables = les composantes principales en projetant selon les vecteurs propres.
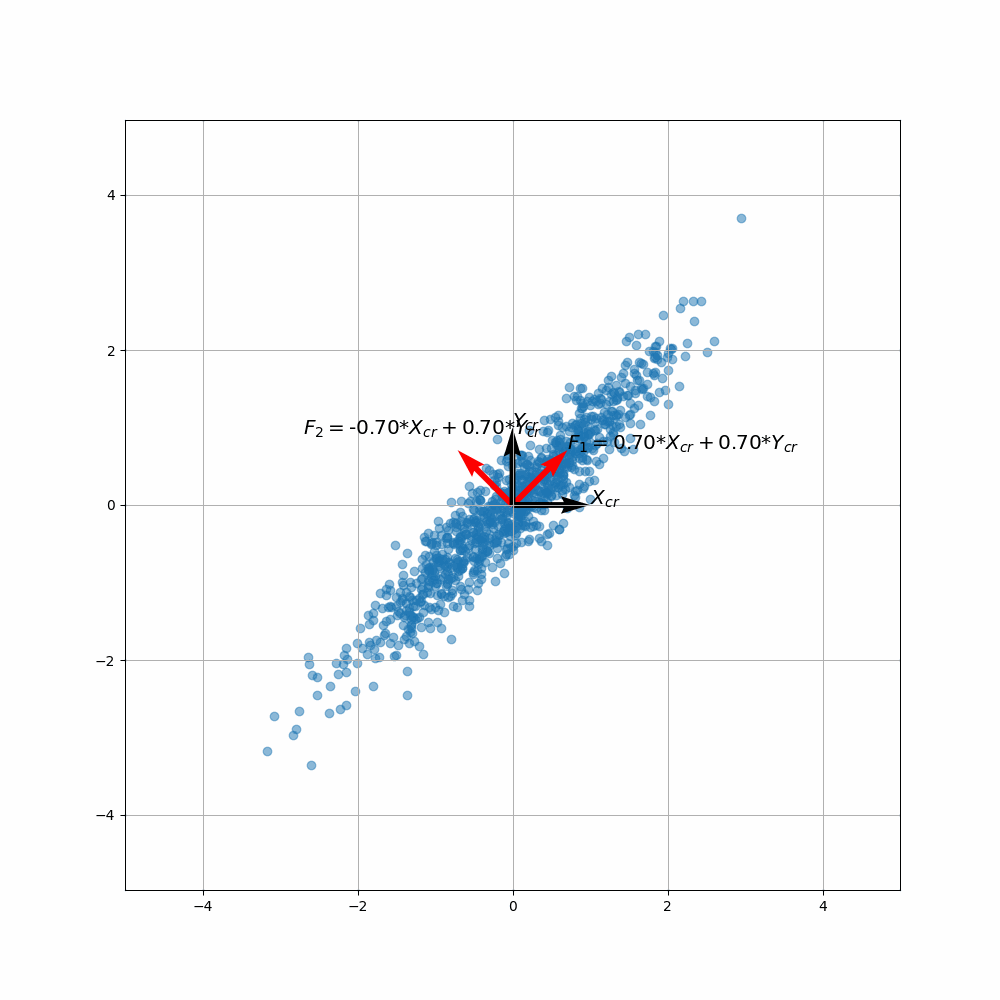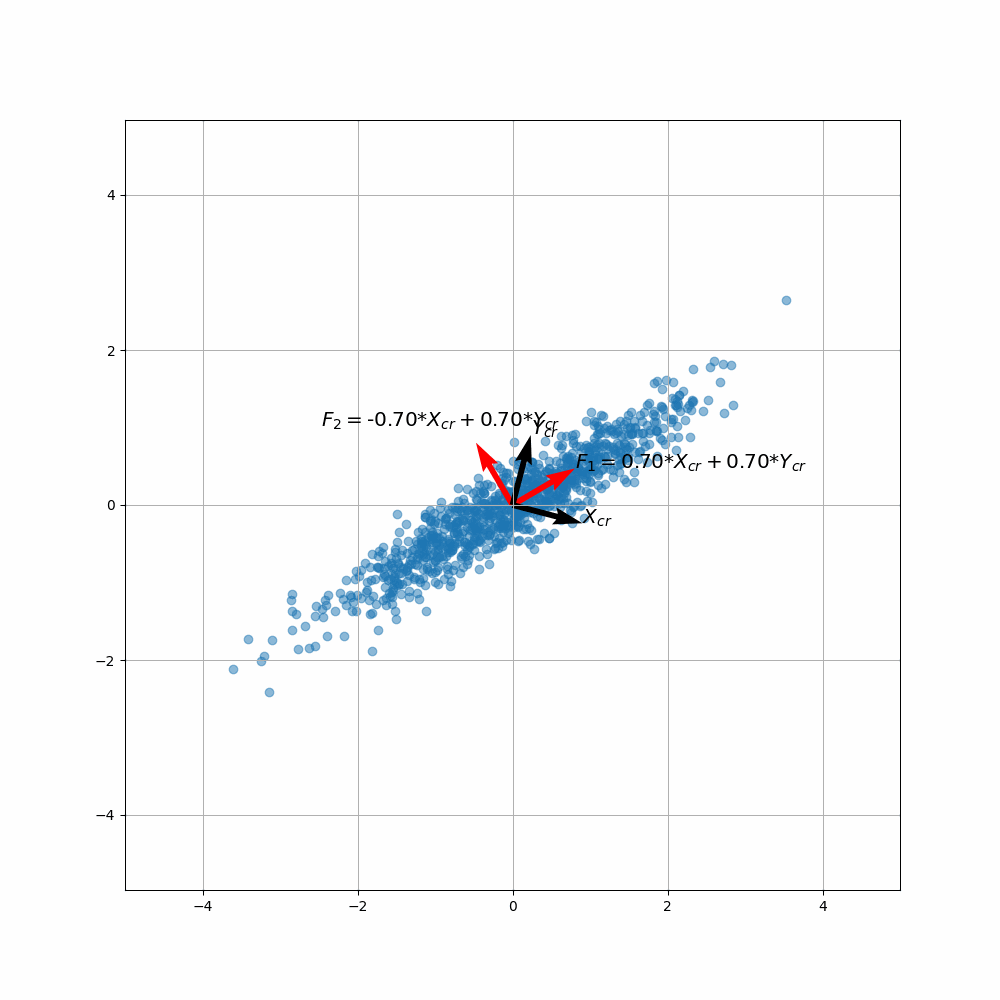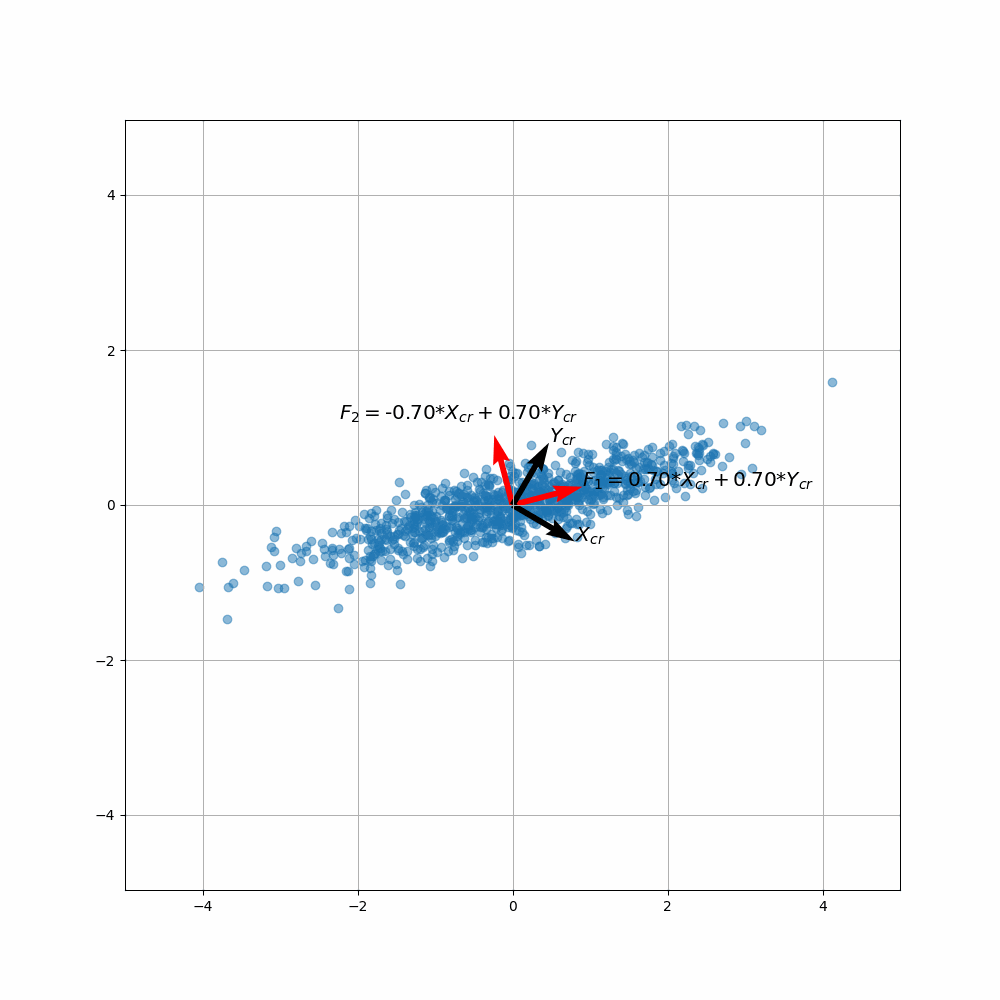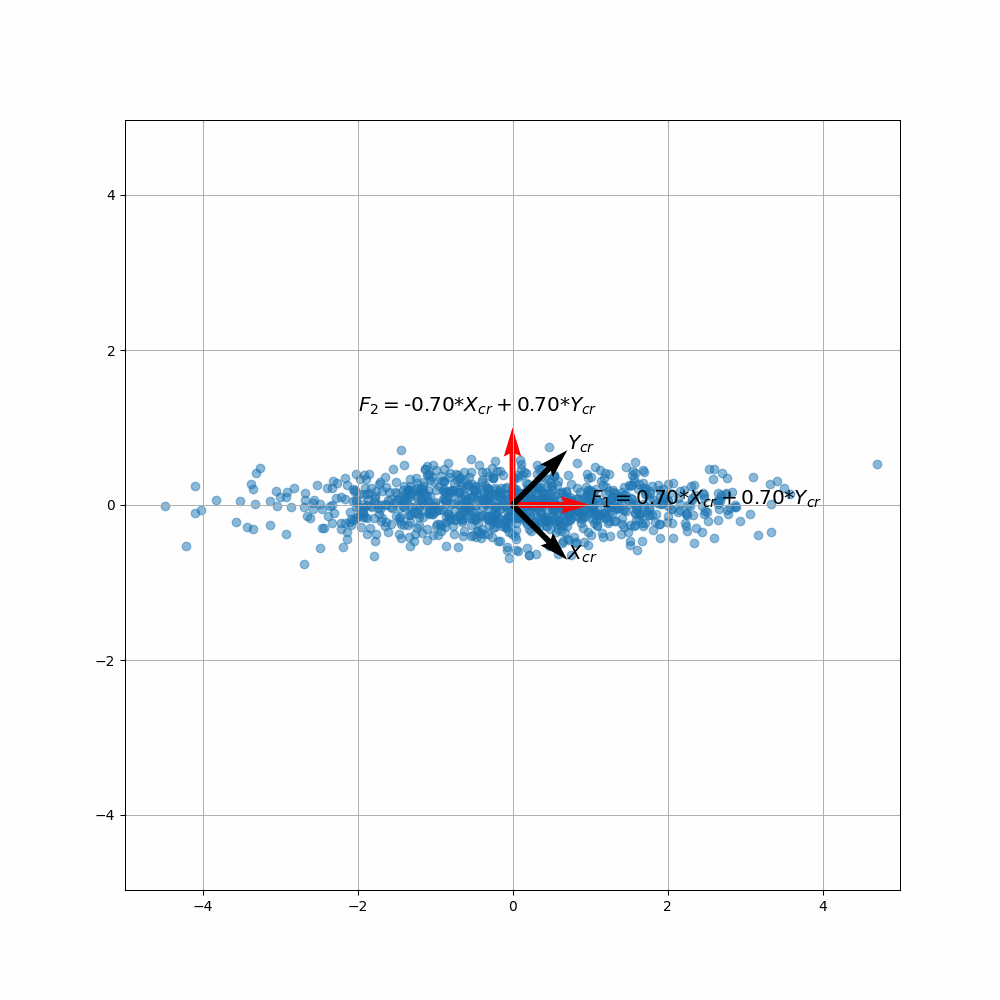
Exemple en 2D
Etape 5 : Réduction du nombre de dimensions.
Basée sur la notion de taux d'inertie : le % d'information porté par chaque axe factoriel.
$TI_j = \frac{\lambda_j}{\sum_{i=0}^M\lambda_i}$
Choix du nombre de dimensions en fonction de l'inertie souhaitée :
- Trier les valeurs propres.
- Garder les p plus grandes valeurs propres, telles que l'inertie conservée $\sum_{j=0}^pTI_j$ soit supérieure à un seuil.
Résumé de la méthode pour M variables.
- Centrer et réduire la matrice de données brutes $\rightarrow \lbrack M_{cr} \rbrack_{N\times M}$
- Calculer la matrice de corrélation $\rightarrow \lbrack COR\rbrack_{M \times M}$
- Rechercher les valeurs propres et les vecteurs propres $\rightarrow \lbrack \lambda\rbrack_{1\times M}, \lbrack V \rbrack_{M \times M}$
- Construction des composantes principales $\rightarrow F_1, F_2...F_M$
- Réduction de dimension $\rightarrow \lbrack TI\rbrack_{1 \times M}; F_1, F_2...F_p$
En python : classe sklearn.decomposition.PCA.
Représentation : cercle de corrélation.
Signification : permet 1) de trouver une signification à chaque composante, 2) de montrer que les composantes séparent les variables en paquets, 3) d'identifier la relation entre les variables
Trois types d'informations peuvent être représentés :
- Les composantes principales : ex F1 et F2
- Coordonnées factorielles des variables
- Coordonnées factorielles des individus
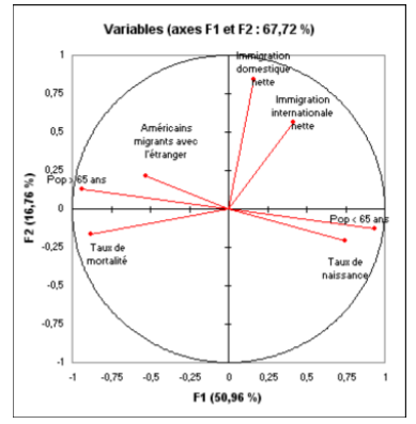
Représentation : cercle de corrélation.
Les axes principaux : $F_1$ et $F_2$
Représentation des variables : Chaque variable $V$ est représenté par un point de cordonnées $(cor(V, F1); cor(V, F2))$
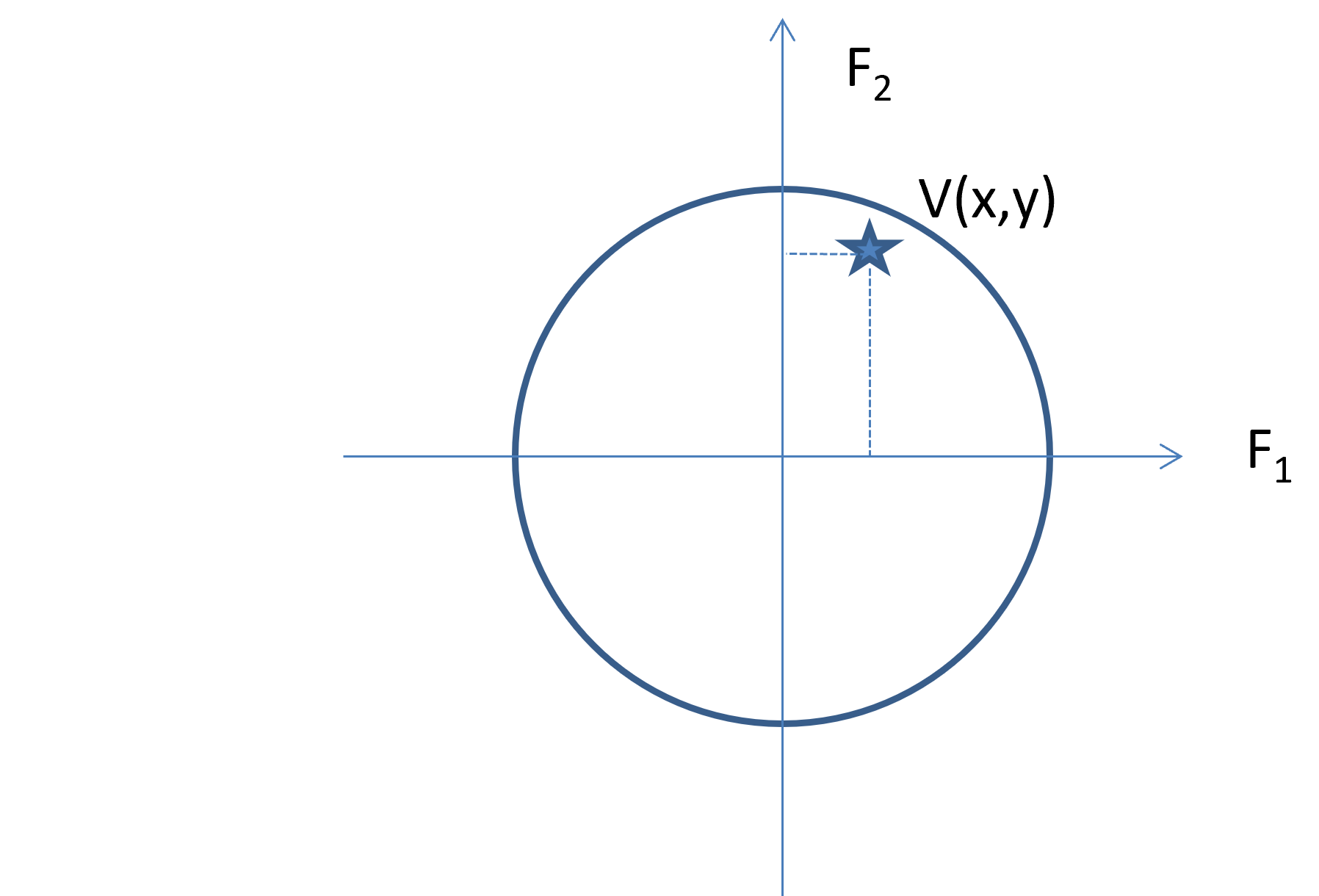
Représentation : cercle de corrélation.
Coordonnées factorielles des variables

Pour chaque variable, on évalue la corrélation entre la variable dans son espace original (centré-réduit) et son nouvel espace
Représentation : cercle de corrélation.
Interprétation
Variables proches du bord du cercle : signifie que la variable est bien corrélée avec un des deux facteurs constituant ce plan $\rightarrow$ variables sont bien représentées par le plan factoriel
Variables proches de 0 : signifie que la variable n’est pas bien corrélée avec un des deux facteurs $\rightarrow$ variables sont mal représentées par le plan factoriel

Représentation : cercle de corrélation.
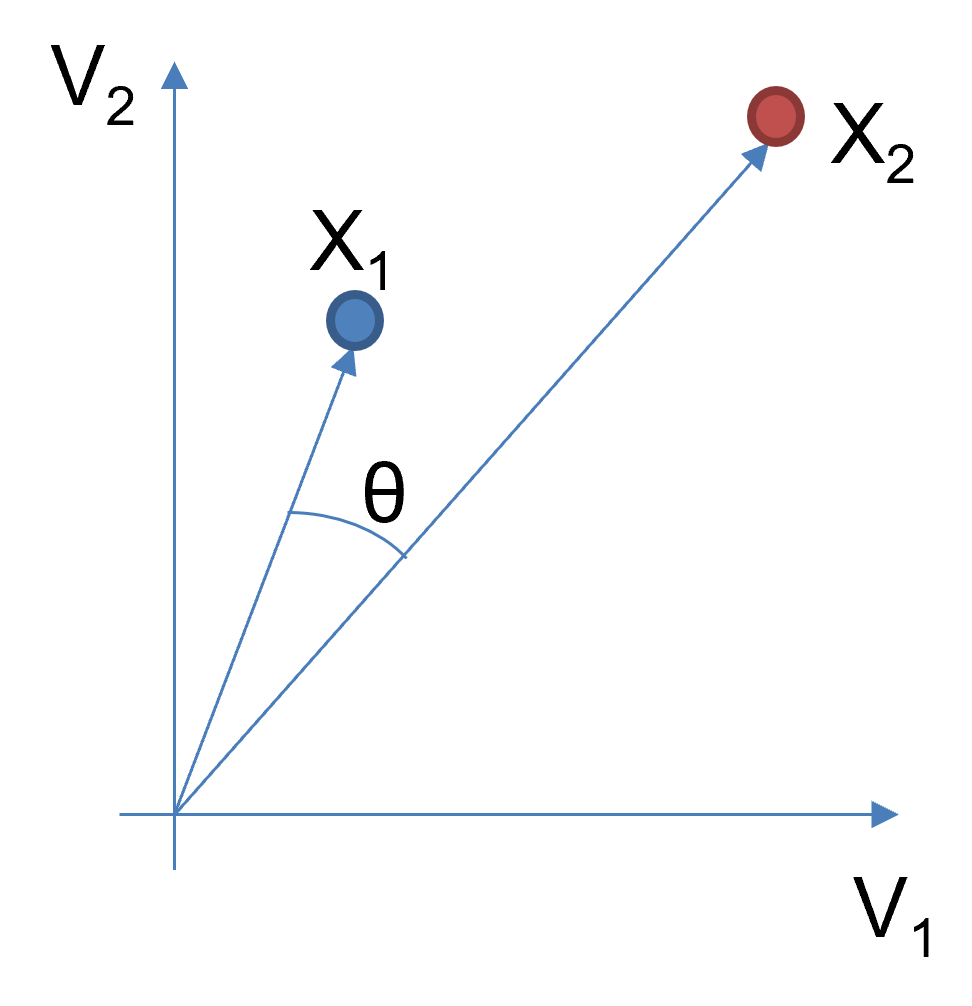
Corrélation linéaire entre deux variables
$r(V_1, V_2) = cos(angle(V_1, V_2))$
Angle proche de 0° : $cos(angle)=r(V_1, V_2)=1$
$\rightarrow V_1$ et $V_2$ sont fortement corrélés positivement.
Angle proche de 90° : $cos(angle)=r(V_1, V_2)=0$
$\rightarrow$ manque de corrélation entre $V_1$ et $V_2$.
Angle proche de 180° : $cos(angle)=r(V_1, V_2)=-1$
$\rightarrow V_1$ et $V_2$ sont fortement corrélés négativement.
$\rightarrow$Identifiez les variables corrélés positivement, négativement, et celles non corrélées.

Représentation : cercle de corrélation.
Représentation des unités spatiales
Les coordonnées factorielle de l'US i pour la composante k :
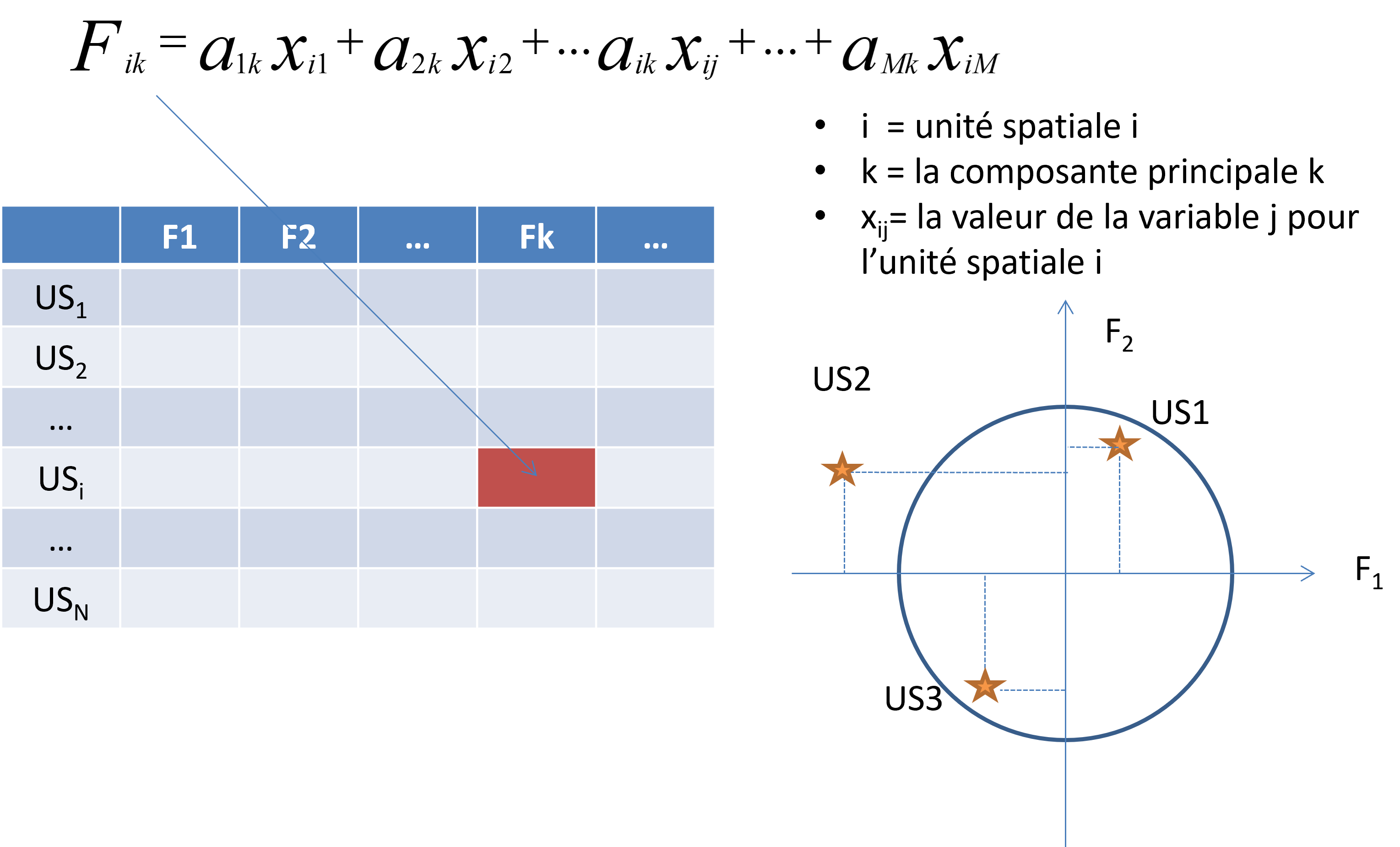
Exemple d'interprétation
ACP appliquée sur un jeu de données caractérisé par :
- 27 unités spatiales représentant des pays d'Europe
- 7 variables :
- L'espérance de vie féminine
- Le revenu moyen par habitant
- La part du budget consacré à la santé
- Le taux de femmes actives
- Le taux d'éducation
- Le taux de chomage
- La mortalité infantile
Exemple d'interprétation
Interprétation des coordonnées factorielles des variables
| Corrélation avec $F_1$ | |
|---|---|
| Esp vie F | 0.86 |
| Pnb/hab | 0.81 |
| % santé | 0.78 |
| Activ F | 0.17 |
| % éducation | 0.10 |
| % chom | -0.62 |
| mort inf | -0.90 |
La première composante principale oppose :
- L’espérance de vie féminine, le revenu moyen par habitant, le % des budgets consacrés à la santé
- Les forts taux de chômage et de mortalité infantile.
Exemple d'interprétation
Interprétation des coordonnées factorielles des individus
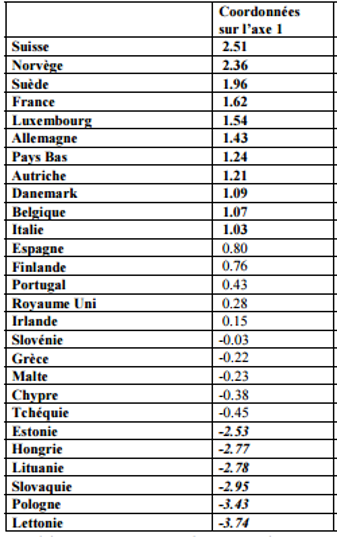
S'opposent des pays :
- Forts pnb/hab et espérance de vie féminine et faible mortalité infantile.
- Faibles pnb/hab et espérance de vie féminine et mortalité infantile relativement forte.
Classification non Supervisée
Classification
Objectif : Regrouper dans des classes les US qui se ressemblent, c-à-d qui possèdent des caractéristiques communes.
- Exemple de classification : couverture des sols, classes : bâti, eau, forêt...
Deux grandes familles de méthodes de classification :
- Supervisée : étant donné un ensemble de classes, la méthode de classification consiste à trouver la meilleure classe pour chaque US.
- Non supervisée : définir des classes non encore identifiées qui groupent les US et leur attribuer une étiquette (« un sens »)
$\rightarrow$ clustering, regroupement
Classification non supervisée
Principe : définir des classes homogènes tout en favorisant l’hétérogénéité entre les classes.
Minimiser la distance entre deux US d’une même classe et maximiser la distance entre deux US de classes différentes.
Étapes
- Choix des données
- Choix de la mesure d'éloignement/ressemblance entre les individus.
- Choix d'un critère d'homogénéité des classes
- Choix d'une méthode de classification
- Mesure de la qualité de la classification
- Interprétation des classes obtenues
Choix des données
- Représenter les variables et étudier leurs corrélations.
- Données brutes, données transformées, composantes factorielles
Choix de la mesure d'éloignement données
- Généralement la distance euclidienne
- Distance de Manhattan
- Distance euclidienne au carré : renforce l'influence des individus "éloignés"
Critère d'homogénéité
On choisit en général l'inertie.
Si l'ensemble des US est regroupé en Q classes :
Inertie totale = inertie intra-classe + inertie intra-classe
Une classe est homogène si son inertie est faible.
Inertie
Si l'ensemble des US est regroupé en Q classes :
Inertie totale = inertie intra-classe + inertie intra-classe
$\sum\limits_{i=1}^N d(X_i, \bar{X})^2 = \sum\limits_{q=1}^Q \sum_{X_i \in q} d(X_i, \bar{X_q})^2 + \sum\limits_{q=1}^Q n_q d(\bar{X_q}, \bar{X})^2$
avec $d(a, b)$ la distance entre $a$ et $b$, $\bar{X}$ la moyenne de $X$, $\bar{X_q}$ la moyenne des individus de la classe q.
Une classe est homogène si son inertie est faible.
Qualité de la partition
Une partition est dite de bonne qualité si :
- les caractéristiques des US de la même classe sont proches $\rightarrow$ variabilité intra-classe faible
- les caractéristiques des US de deux classes différentes sont éloignées $\rightarrow$ variabilité inter classe forte
La qualité d'une partition est mesurée par :
Q = Inertie inter classe / inertie totale- Q=1, les individus de chaque classe sont identiques ou nb de classes=nb d’individus
- Q=0, une seule partition ou la moyenne de chaque cluster est égale à celle de l'ensemble des données $\rightarrow$ les clusters ne séparent pas du tout les données
- Q proche de 1 : meilleure partition
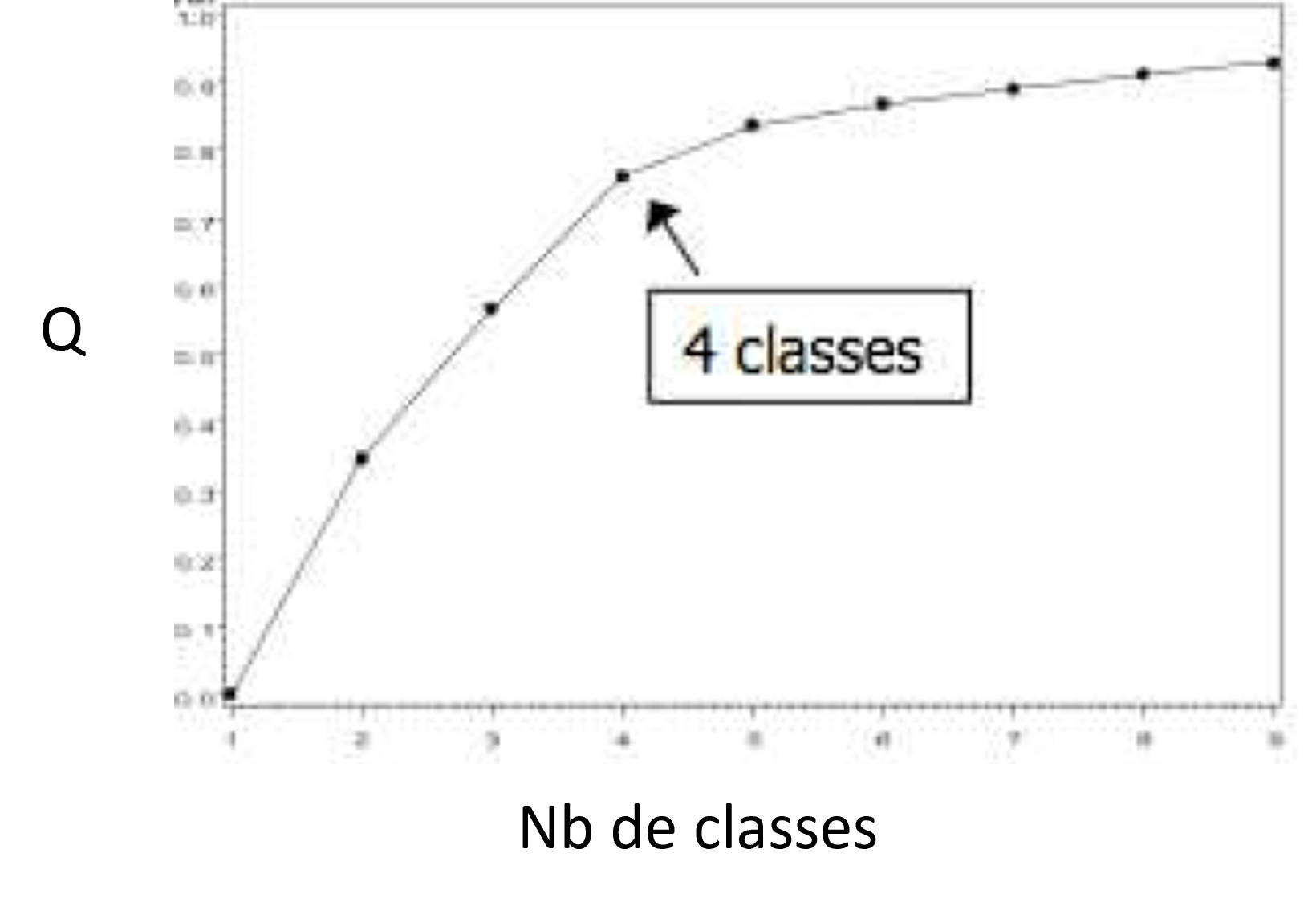
Qualité de la partition - représentation
La qualité d'une partition est mesurée par :
Q = Inertie inter classe / inertie totaleQ doit être le plus proche de 1 sans avoir un nombre de classes élevé
$\rightarrow$s'arrêter après un dernier saut important
Choix d'une méthode de classification
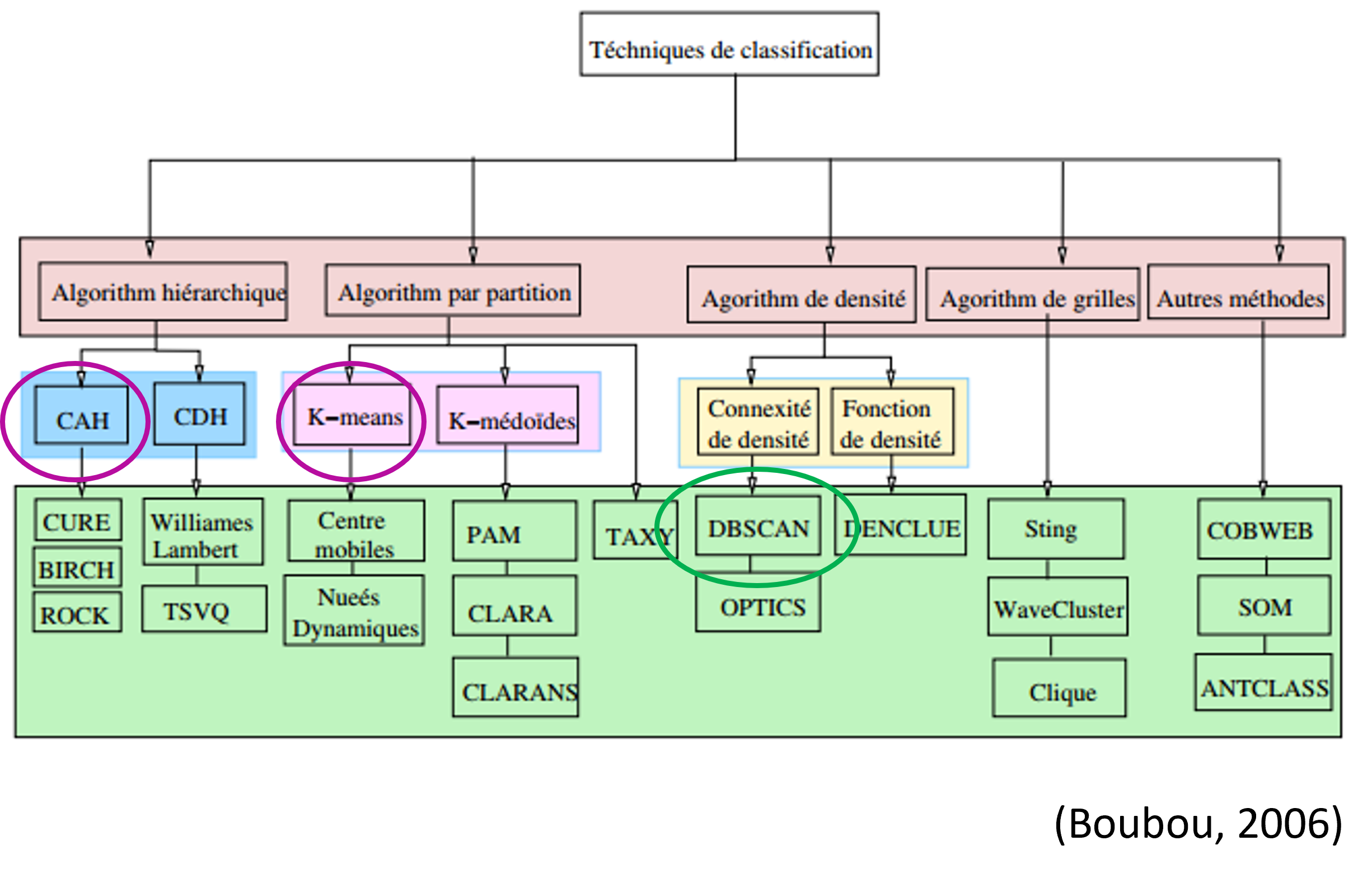
Principales familles de méthodes de regroupement
- Méthodes hiérarchiques
Consiste à créer une décomposition hiérarchique par agglomération ou division de groupes similaires ou dissimilaires - Méthodes par partitionnement
Construire k partitions et les améliorer jusqu'à obtenir une similarité satisfaisante - Méthodes basées sur la densitéAnalyse de dynamiques spatiotemporelles
Consiste à grouper les US tant que la densité de voisinage excède une certaine limite - Méthodes basées sur la grille
Consiste à diviser l'espaces en cellules formant une grille multi-niveaux et grouper les cellules voisines en termes de distance - Autres : basées sur le modèle ou l'apprentissage
SOM, COBWEB, réseaux de neurones
Clustering ascendant hierarchique (CAH)
Objectif :Définir un arbre hierarchique (dendrogramme) permettant :
- Un regroupement progressif, ne révise pas les classes regroupées
- La mise en évidence de liens hiérarchiques entre US ou groupes d'US
- La détection d'un nombre de classes intuitif et naturel au sein d'une population : distance inter classe est grande
Clustering ascendant hierarchique (CAH)
Objectif :Définir un arbre hierarchique (dendrogramme) permettant :
- Un regroupement progressif, ne révise pas les classes regroupées
- La mise en évidence de liens hiérarchiques entre US ou groupes d'US
- La détection d'un nombre de classes intuitif et naturel au sein d'une population : distance inter classe est grande
Clustering ascendant hierarchique (CAH)
Objectif :Définir un arbre hierarchique (dendrogramme) permettant :
- Un regroupement progressif, ne révise pas les classes regroupées
- La mise en évidence de liens hiérarchiques entre US ou groupes d'US
- La détection d'un nombre de classes intuitif et naturel au sein d'une population : distance inter classe est grande
CAH - Algorithme
- Etape 1 : initialisation
- Partition en N singletons : chaque US constitue une classe
- Calculer la matrice de leur distances deux à deux
- d(i,j) représente la dissimilarité entre les individus i et j.
- matrice symétrique avec des zéros sur la diagonale $\rightarrow$ seule une moitié est nécessaire.
- Itération :besoin de : distance et indice d'agrégation
- Regrouper les deux classes les plus proches au sens de la "distance" entre les classes.
- Mettre à jour la matrice des distances en remplaçant les deux classes regroupées par la nouvelle et en calculant sa "distance" avec chacune des autres classes.
- Etape finale : l'algorithme s'arrête avec l'obtention d’une seule classe.
Indice d'agrégation
Indice d'agrégation
On regroupe les classes en minimisant l'indice d'agrégation.
Soit A et B deux classes ou 2 US d'une partition donnée :
- Critère du saut minimal ou minimal linkage : la plus petite distance entre deux US de classes différentes
$d(A,B)=min(d_{ij}), i\in A, j\in B$ - Critère du saut maximal ou maximal linkage : la plus grande distance entre deux US de classes différentes
$d(A,B)=max(d_{ij}), i\in A, j\in B$ - Critère de la moyenne : la moyenne de toutes les distances calculées entre chaque US d’une classe A et chaque US d’une classe B
$d(A,B)=\frac{1}{card(A)card(B)}$$\sum_{i\in A, j\in B}$$ d_{ij}$
Indice d'agrégation - exemple
- Unité spatiales : A, B, C, D, E, F, G
- Déterminer le dendrogramme étant donné les distances entre les unités spatiales
- Indice d'agrégation : critère du saut minimal
Indice d'agrégation
- Critère de Ward - Saut de Ward :
- Basé sur la notion d’inertie : gain minimum d’inertie intra-classe à chaque agrégation et une perte d’inertie interclasse due à cette agrégation.
- Le critère de Ward consiste à choisir à chaque étape le regroupement de deux classes A et B tel que l’augmentation de l’inertie intra-classe soit minimale. $d(A,B)=\frac{card(A)card(B)}{card(A)+card(B)}d(g_A, g_B)^2$
- $g_A$ et $g_B$ : les centres de gravité des classes A et B.
- Minimiser $d(A, B)$ :
- choisir les classes dont les centres de gravité sont proches : $d(g_A,g_B)^2$ petit ET
- des classes d’effectifs faibles : $\frac{card(A)card(B)}{card(A)+card(B)}$ petit;
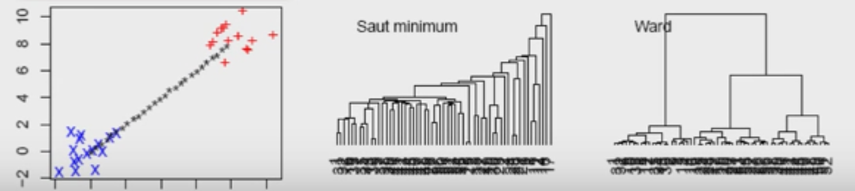
Indice d'agrégation
- Critère minimal :
- On regroupe des classes de proche en proche $\rightarrow$ souvent : un grand groupe comportant beaucoup d’individus et des petits groupes séparés.
- Produit des dendrogrammes peu harmonieux
- Critère maximal :
- On regroupe des classes de proche en proche.
- Produit des dendrogrammes harmonieux c-a-d que les classes ont des effectifs pas trop différents
- Sensible aux outliers
- Critère de Ward :
- Optimisation pas à pas $\rightarrow$ Ne dépend pas d’un choix initial arbitraire
- Produit des arbres harmonieux
Dendrogramme en Python
from sklearn.datasets import load_iris
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
iris = load_iris()
Z = linkage(iris.data, 'ward')
plt.figure(figsize=(18, 8))
dn = dendrogram(Z)
plt.show()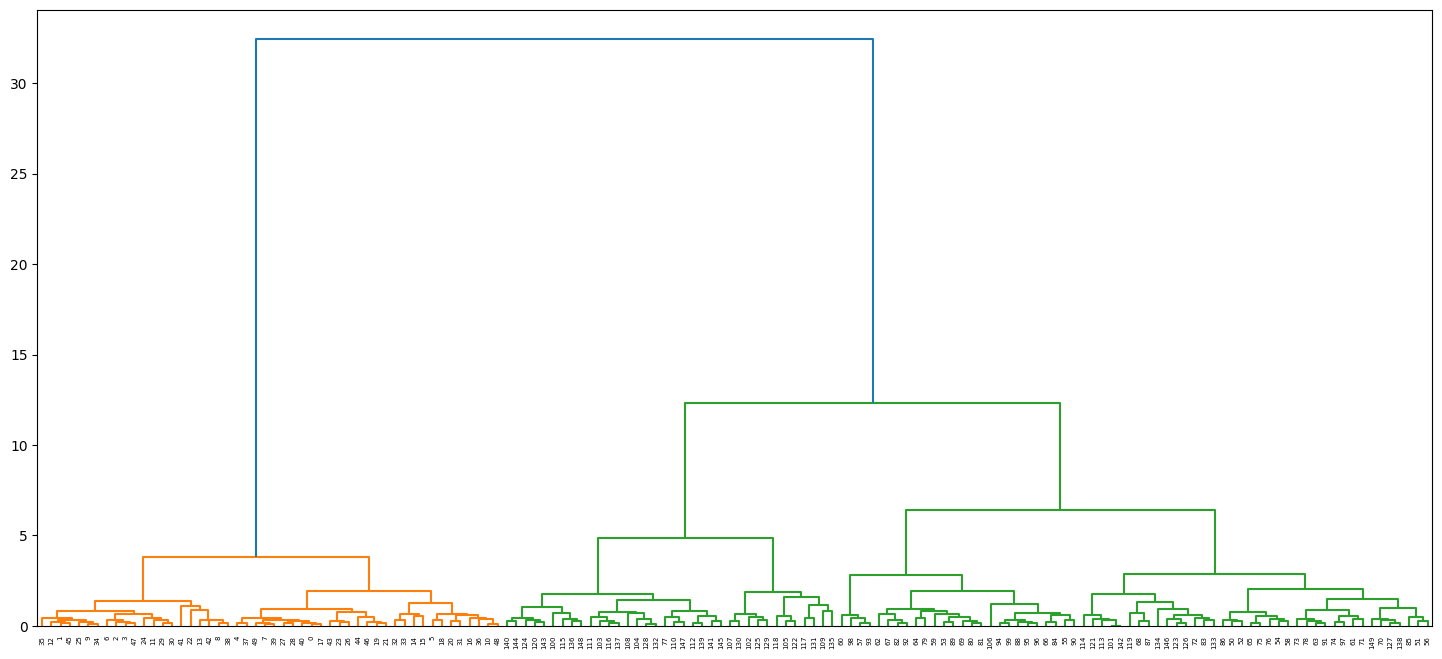
CAH en Python
from sklearn.datasets import load_iris
from sklearn.cluster import AgglomerativeClustering
iris = load_iris()
model = AgglomerativeClustering(n_clusters=3)
labels = model.fit_predict(iris.data)
plt.scatter(iris.data[:,0], iris.data[:,2], c=labels)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[2])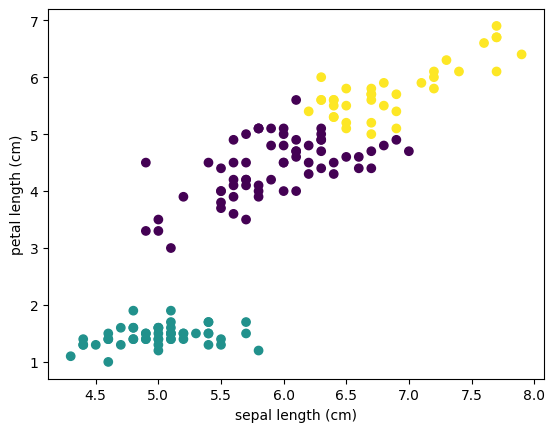
CAH avec contraintes de proximité spatiale
CAH : forte dispersion géographique des classes obtenues.
CAH avec contraintes de proximité spatiale : introduction de l'information spatiale dans la classification
- Matrice de voisinage entre les US : Vij = 1 si i et j sont voisins, 0 sinon.
- Matrice de distances géographiques entre US.
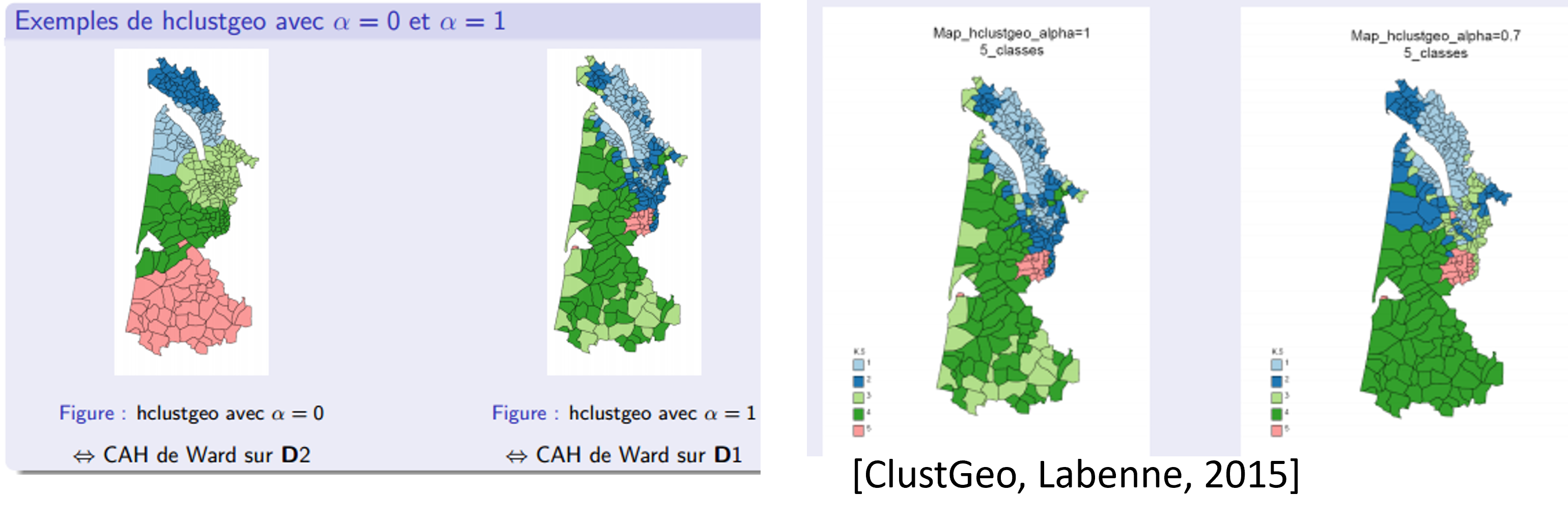
L'algorithme HClustGeo permet de prendre en compte l'information géographique :
- Introduction d’un coefficient α au sein de la CAH de Ward [ClustGeo, Labenne, 2015]
CAH avec contraintes de proximité spatiale
- Deux matrices de distances
- $D_{1 [N\times N]}$ = matrice de distances euclidiennes entre les US, calculée à partir de la matrice de données décrite par les M variables quantitatives
- $D_{2 [N\times N]}$ = matrice de distances géographiques entre les US
- Deux mesures de Ward calculées pour $D_1$ et $D_2$
- $d_1(A, B) = \frac{card(A)card(B)}{card(A)+card(B)}d_1(g^1_A, g^1_B)^2$
- $d_2(A, B) = \frac{card(A)card(B)}{card(A)+card(B)}d_2(g^2_A, g^2_B)^2$
- Mesure d'agrégation totale
$d(A, B) = \alpha d_1(A, B) + (1 - \alpha) d_2(A, B)$
- $\alpha = 0$, une CAH de Ward est calculée uniquement sur la matrice de distances $D_2$
- $\alpha = 1$, une CAH de Ward est calculée uniquement sur la matrice de distances $D_1$
CAH avec contraintes de proximité spatiale
Le choix du paramètre $\alpha$ est très important :
- Caractériser chaque partition par les indices de qualités $Q_1$ et $Q_2$
- Choisir comme référence la valeur de Q1 calculée avec α = 1 (CAH de Ward sur D1).
- Choisir le plus petit $\alpha$ possible tel que la valeur de $Q_1$ soit la moins dégradée possible.
Algorithmes de partitionnement
Classification par partition : construit une partition en K classes à partir de l'ensemble des US
Principe :
- Nombre K de classes à choisir a priori (on peut utiliser une CAH pour choisir k)
- Génération d'une partition initiale, puis révision : améliorer en attribuant les US d'une classe à l'autre.
- Basée sur les maximums locaux en optimisant une fonction objectif
- Les US doivent être :
- "similaires" au sein d'une même classe.
- "dissimilaires" entre deux classes différentes.
K-moyennes - Algorithme des centres mobiles
K-moyennes en Python
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
iris = load_iris()
k_means = KMeans(n_clusters=3)
labels = k_means.fit_predict(iris.data)
plt.scatter(iris.data[:,0], iris.data[:,2], c=labels)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[2])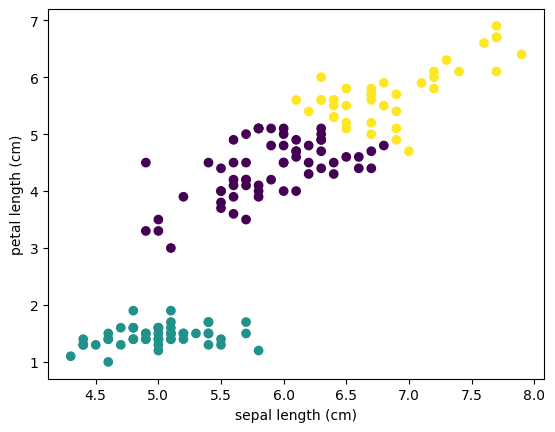
Algorithmes de partitionnement
Avantages
- Simple à mettre en place
- Compréhensible
- Applicable à des données de grande taille
Inconvénients
- Le nombre de classes doit être choisi a priori
- Instable : dépendance au choix des centres initiaux
- Mauvaise prise en compte des "outliers" : points extrêmes en dehors des groupes; peut fausser les moyennes et donc les centres.
- Convergence plus ou moins rapide
Algorithmes par densité : DBSCAN
Avantages
- Algorithme simple, pas besoin de fournir le nombre de clusters.
- Est capable de détecter et exclure les données abbérantes.
Inconvénients
- Les clusters sont supposés avoir la même densité.
- Certains US ne sont pas clusterisés.
Deux paramètres :
- $\epsilon$ la distance de recherche des voisins
- Min_pts : le nombre minimal de voisins dans le rayon $\epsilon$ pour que le point soit attribué au cluster
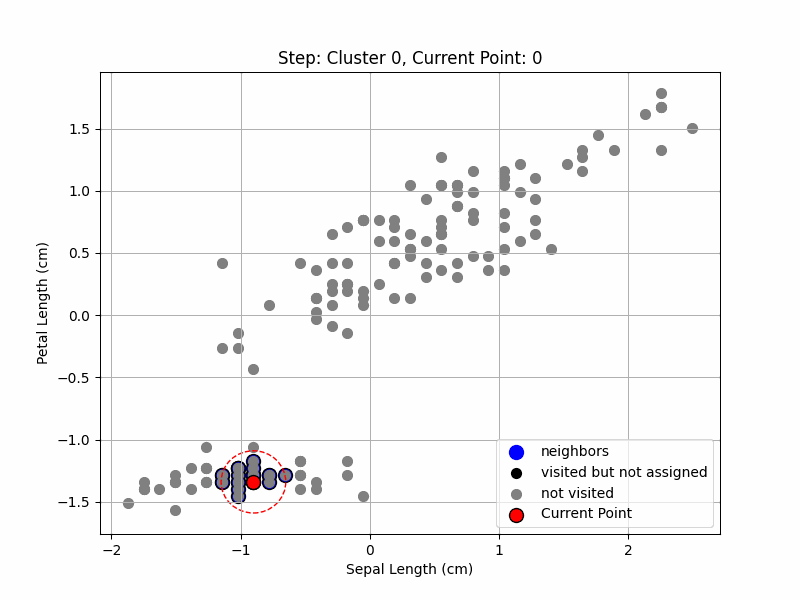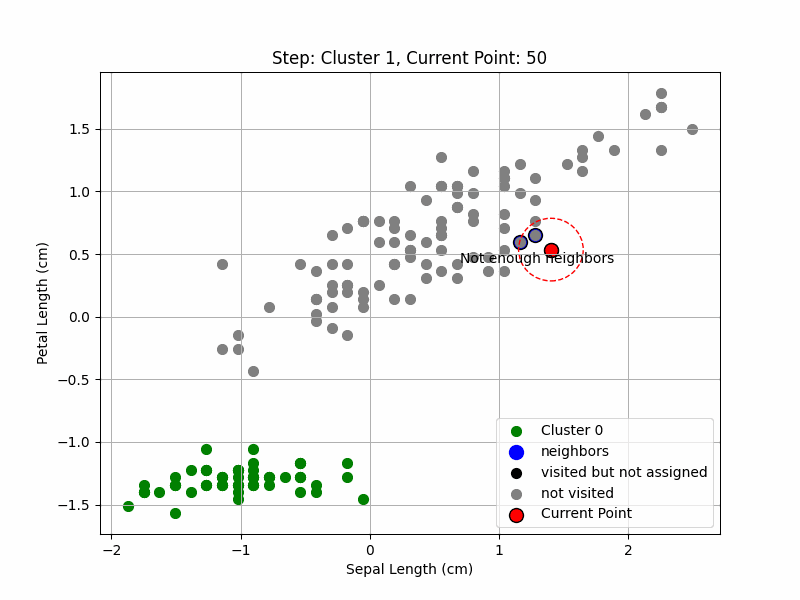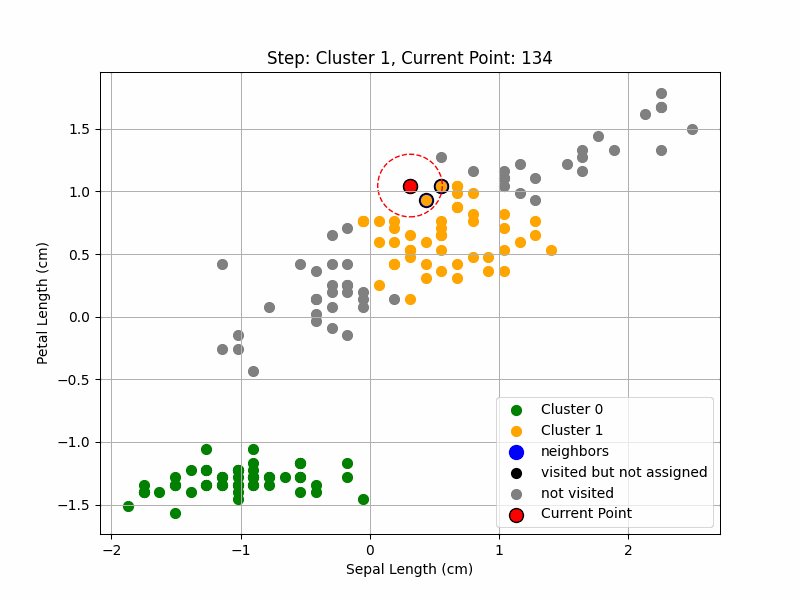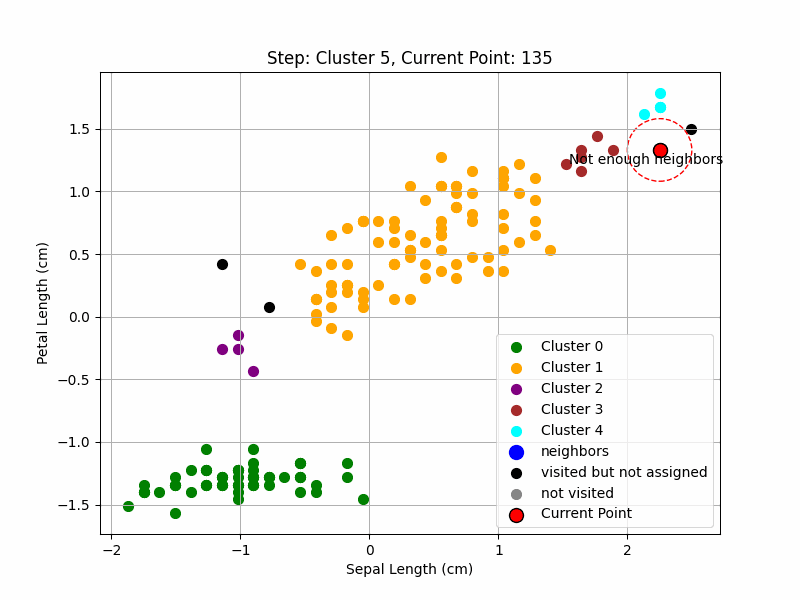
Algorithme de DBSCAN
initialisation
- Marquer tous les points comme non-visités.
Parcours des points
- Pour chaque point non visité, le marquer comme visité et trouver ses voisins dans le rayon $\epsilon$.
Formation de cluster
- Si le nombre de voisins est inférieur à Min_pts, marquer le point comme bruit (point isolé ou "noise")
- Sinon, commencer un nouveau cluster en assignant ce point et en ajoutant ses voisins directs à une "queue" à explorer.
Expansion du cluster
- Pour chaque point de la "queue", s'il n'a pas été visité, le marquer comme visité et rechercher ses voisins.
- Si ce point a au moins Min_pts voisins, les ajouter à la "queue" pour continuer l'expansion.
- Assigner tous ces points non encore attribués au cluster en cours.
Réitération
- Recommencer le processus jusqu'à ce que tous les points soient visités.
Résultat final
- Les points non assignés à des clusters sont considérés comme du bruit.
- Les clusters finaux sont formés par les points densément connectés.
Algorithme de DBSCAN
Quel algorithme de clustering choisir ?
Certains algorithmes sont plus ou moins adaptés à certaines formes de groupe $\rightarrow$ Regarder la forme des groupes sur le nuage de points des deux premières composantes de l'ACP.
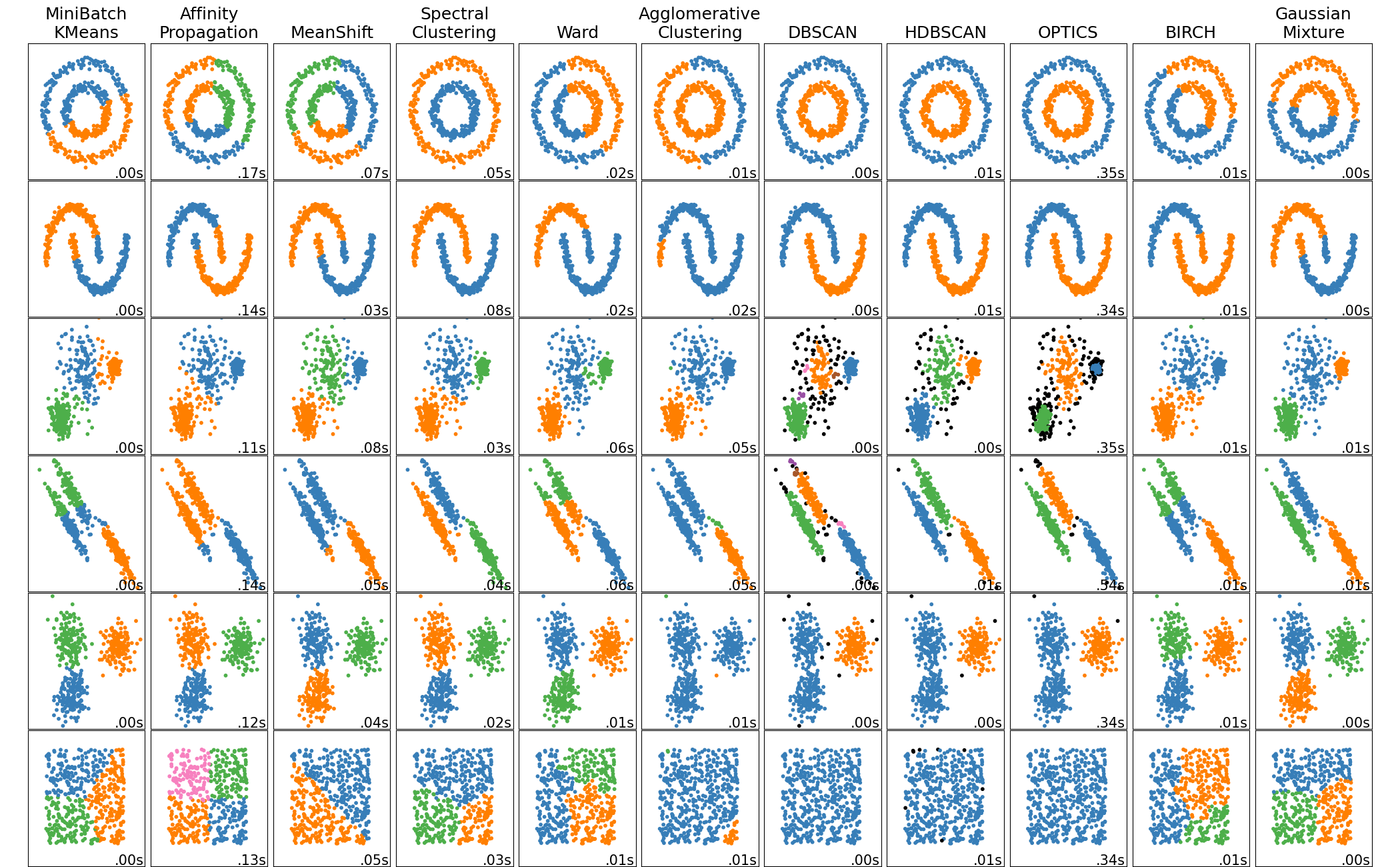
[scikit-learn documentation]
Classification Supervisée
Classification Supervisée - Principe
On veut classifier des données en K classes connues, pour lesquelles on dispose d'exemples.
Un algorithme d'apprentissage automatique est entrainé sur ces exemples, puis est utilisé pour inférer la classe des individus.
- Jeu d'entrainement = jeu de données sur lequel est entrainé le modèle.
- Jeu de validation = jeu sur lequel on ajuste les hyperparamètres du modèle (hyperparameter tuning).
- Jeu de test (ou d'évaluation) = jeu sur lequel la qualité du classifieur est évaluée.
Le jeu de test doit être strictement distinct du jeu d'entrainement, pour éviter la "fuite de données" (data leakage) qui biaise le test.
Attention à l'autocorrélation spatiale ! [Karasiak 2022]
Métriques d'évaluation
Matrice de confusion $M_{i,j}$ = nombre d'individus de la classe i prédits dans la classe j
Métriques par classe :
- Rappel (Producer accuracy) ${PA}_i=\frac{M_{i,i}}{\sum_{j} M_{i,j}}$
- Précision (User accuracy) ${UA}_i=\frac{M_{i,i}}{\sum_{j} M_{j,i}}$
- F1-score ${F1}_i\ =\ 2\frac{{UA}_i\ \times\ {PA}_i}{{UA}_i\ +\ {PA}_i}=\frac{2\ \ast\ M_{i,i}}{\sum_{j} M_{i,j}+\ \sum_{j} M_{j,i}}$
- ...
Métriques globales :
Rappel moyen $PA = \frac{1}{n}\sum_{i=1}^{n}{PA_i}$, Precision moyenne, F-1 score moyen, Exactitude (Overall accuracy) $OA = \frac{\sum_{i} M_{i,i}}{N}$...
Exemple: classification sur 3 classes
| Classe réelle ↓ / prédite → | A | B | C |
|---|---|---|---|
| A | 95 | 0 | 5 |
| B | 3 | 30 | 17 |
| C | 2 | 4 | 44 |
Sur un total de N = 200 échantillons.
- Rappel (PA) : A = 95/100 = 0.95, B = 30/50 = 0.60, C = 44/50 = 0.88
- Précision (UA) : A = 95/50 = 0.100, B = 30/34 = 0.88, C = 44/66 = 0.67
- F1-score : A = $\frac{2\times 95}{100+100}$=0.95, B = 0.71, C = 0.76
Métriques globales :
- Exactitude (Overall Accuracy) OA = $\frac{95+30+44}{150}$ = 0.85
- F1-score moyen = $\frac{0.95+0.71+0.76}{3}$ = 0.81
Familles d'algorithmes supervisés
Les algorithmes de classification supervisée se divisent en plusieurs familles basées sur des approches distinctes :
- Modèles Linéaires : Ex : Régression Logistique, Analyse Discriminante Linéaire (LDA)
- Modèles Basés sur les Arbres : Ex : Arbres de Décision, Forêt Aléatoire, Gradient Boosting
- Machines à Vecteurs de Support (SVM) : Classifieurs avec des marges maximales
- Apprentissage Instance-Based : Ex : k-Nearest Neighbors (k-NN)
- Algorithmes Bayésiens : Ex : Naive Bayes, Réseaux Bayésiens
- Réseaux de Neurones : Ex : Multilayer Perceptron (MLP), CNN, RNN
- Algorithmes Basés sur des Règles : Ex : RIPPER
Exemple d'Algorithme : Random Forest
Random Forest est un modèle d'ensemble d'arbres de décision qui utilise le bagging pour améliorer la précision.
Caractéristiques principales :
- Ensemble de plusieurs arbres de décision : Chaque arbre est construit sur un échantillon aléatoire du jeu de données.
- Décisions basées sur le vote majoritaire : La classe prédite est celle choisie par la majorité des arbres.
- Réduction de l'overfitting : En combinant plusieurs modèles, Random Forest augmente la robustesse et la généralisation.
- Importance des caractéristiques : Permet de mesurer l'influence de chaque variable sur la prédiction.
Avantages : Résistant au bruit, flexible, et performant pour des problèmes non linéaires.
Fonctionnement de Random Forest
Etapes :
- Créer plusieurs sous-échantillons du jeu de données (échantillonnage bootstrap).
- Construire un arbre de décision sur chaque échantillon.
- Prédire une nouvelle instance en faisant voter tous les arbres et choisir la classe majoritaire.
Chaque arbre est ainsi légèrement différent, ce qui réduit la corrélation entre eux et augmente la robustesse globale du modèle.
Construction d'un Arbre de Décision dans Random Forest
La construction d'un arbre de décision dans une Random Forest se fait de la manière suivante :
- Échantillonnage Bootstrap : Créer un échantillon aléatoire avec remplacement à partir du jeu de données d'origine.
- Construction de l'arbre : Pour chaque nœud de l'arbre :
- Sélectionner aléatoirement un sous-ensemble de variables (features).
- Évaluer la meilleure variable et le seuil parmi ce sous-ensemble pour séparer les données.
- Diviser le nœud en utilisant cette variable.
- Arrêt de la construction : Continuer la division jusqu'à atteindre un critère d'arrêt (profondeur maximale, nombre minimum d'échantillons).
Exemple : Construction d'un Arbre de Décision
| Longueur des pétales | Largeur des pétales | Espèce |
|---|---|---|
| 1.4 | 0.2 | Setosa |
| 4.7 | 1.4 | Versicolor |
| 5.1 | 1.8 | Versicolor |
| 1.5 | 0.1 | Setosa |
| 4.9 | 1.5 | Versicolor |
| 5.8 | 2.2 | Virginica |
Indice de Gini
L'indice de Gini mesure l'impureté d'un nœud. Il est défini par :
$Gini = \sum_{i=1}^{C} p_i(1 - p_i) = 1 - \sum_{i=1}^{C} p_i^2$
- pi est la proportion des instances appartenant à la classe i dans le nœud.
- Un Gini de 0 indique que le nœud est pur (toutes les instances appartiennent à une seule classe).
- Un Gini proche de 0.5 indique une forte impureté (les classes sont mélangées).
Calcul de l'Indice de Gini : Exemple
Exemple : on sépare le jeu de données en fonction de la longueur du pétale < 1.6:
| Longueur des pétales | Largeur des pétales | Espèce |
|---|---|---|
| 1.4 | 0.2 | Setosa |
| 4.7 | 1.4 | Versicolor |
| 5.1 | 1.8 | Versicolor |
| 1.5 | 0.1 | Setosa |
| 4.9 | 1.5 | Versicolor |
| 5.8 | 2.2 | Virginica |
- Nœud de gauche: 2 instances (2 Setosa)
- Nœud de droite: 4 instances (3 Versicolor, 1 Virginica)
Calcul du Gini pour le nœud gauche :
$Gini = 1 - (2/2)^2 = 0 \rightarrow$ Ce nœud est pur !
Calcul du Gini pour le nœud droit :
$Gini = 1 - (3/4)^2 - (1/4)^2 = 0.375$
Le Gini total pour cette division est la moyenne pondérée des deux nœuds =0.25.
Choix de la Division
Parmi toutes les divisions possibles, l'arbre de décision choisit celle qui minimise l'indice de Gini.
Dans cet exemple, si la division par la longueur du pétale minimise le Gini, alors l'arbre utilisera cette caractéristique pour créer un nœud de décision.
Itération : Le processus se répète jusqu'à ce qu'un critère d'arrêt soit atteint (profondeur maximale, impureté minimale, etc.).
Random Forest en Python
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
iris = load_iris()#Load the dataset
clf = RandomForestClassifier()#construct the classifier
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target,
train_size=0.5)
clf.fit(X_train, y_train)#train the classifier
y_pred = clf.predict(X_test)
print(classification_report(y_test, y_pred)) precision recall f1-score support
setosa 1.00 1.00 1.00 27
versicolor 0.96 0.96 0.96 27
virginica 0.95 0.95 0.95 21
accuracy 0.97 75
macro avg 0.97 0.97 0.97 75
weighted avg 0.97 0.97 0.97 75