Analyse Univariée

M2 IGAST

Martin Cubaud

LASTIG-UGE-IGN/ENSG

2024-2025

Analyse Univariée

Décrire et mesurer la répartition des valeurs que peut prendre une variable : sa distribution (≈ “histogramme en continu”)

Parfois certaines distributions ressemblent à des distributions bien connues : on parle de lois.

e.g. loi normale/gaussienne, loi de Poisson, géométrique, exponentielle…

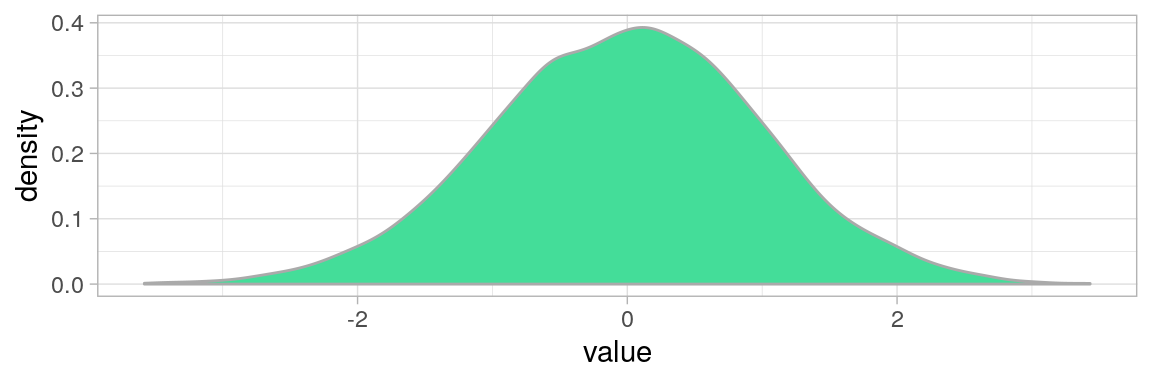
Histogramme d'une variable suivant une loi normale $\mathcal{N}(0, 1)$

xx = np.random.normal(size=2600)
plt.figure(figsize=(12, 5))
plt.hist(xx, bins=50, edgecolor="#aaaaaa", color="#44DD99")
plt.xlabel("value")
plt.ylabel("count")
plt.grid(True)
plt.show()

xx = pd.DataFrame(np.random.normal(size=2600))
xx.hist(bins=50, figsize=(12, 5), edgecolor="#aaaaaa", color="#44DD99", grid=True)
plt.xlabel("value")
plt.ylabel("count")
plt.show()

xx <- data.frame(value=rnorm(2600))
plot1 <- ggplot(xx)+
		geom_histogram(aes(x = value),bins = 50, color="#aaaaaa", fill="#44DD99" )+
		theme_light()
plot1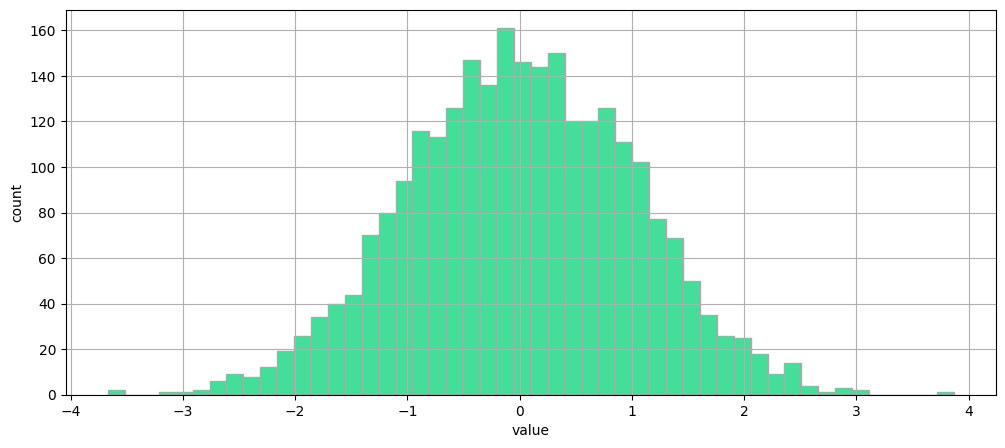

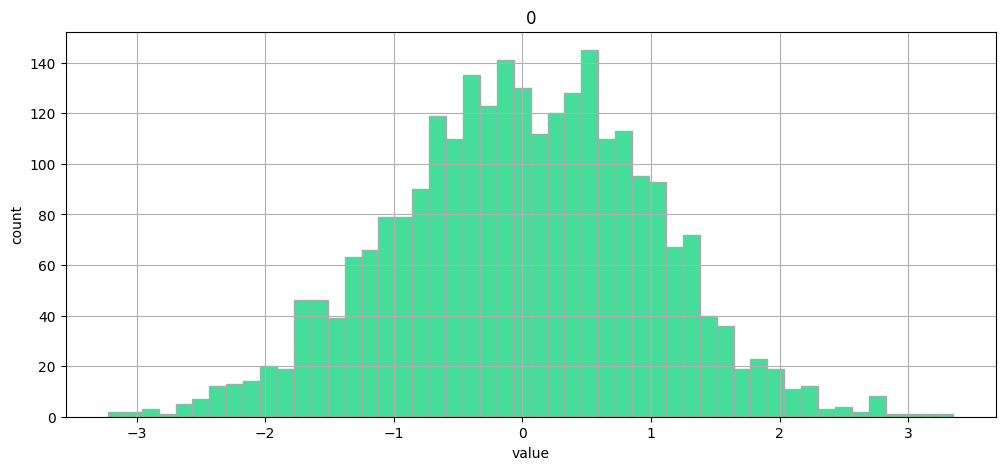
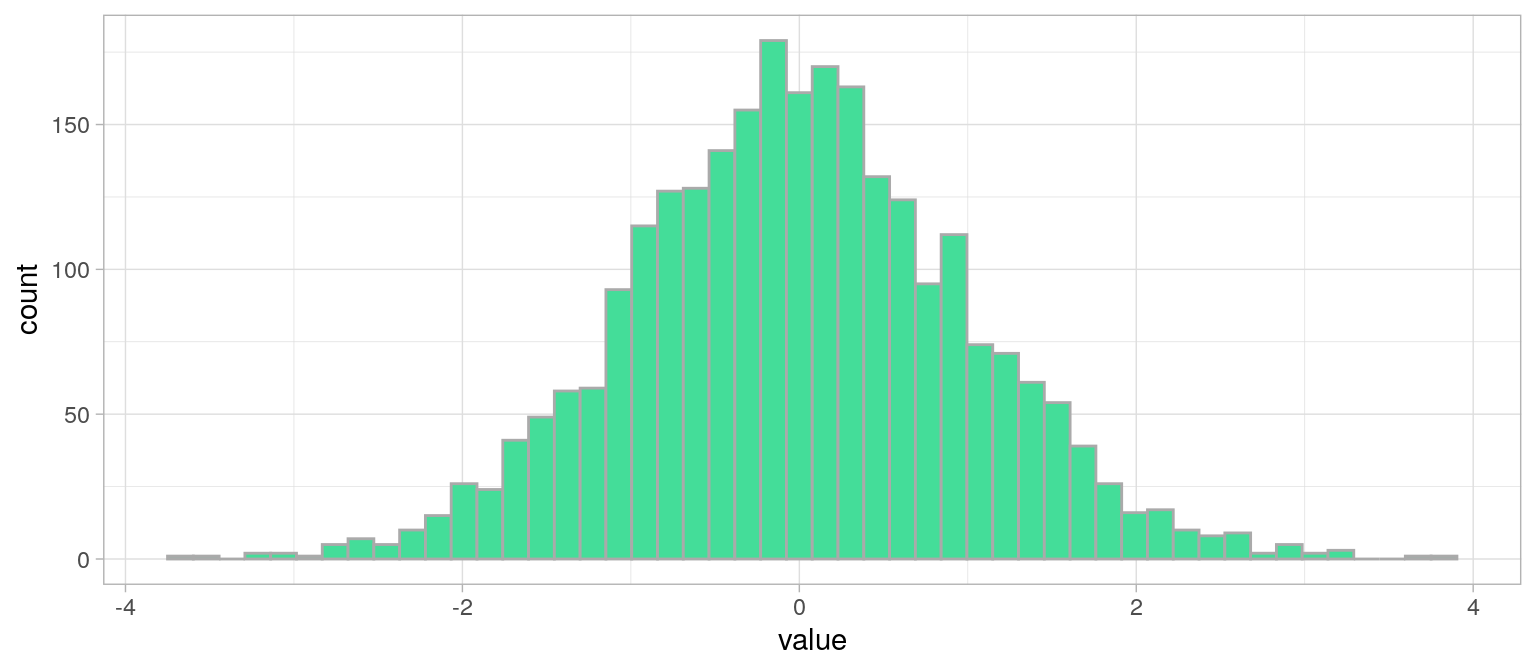
Histogramme d'une distribution
réelle

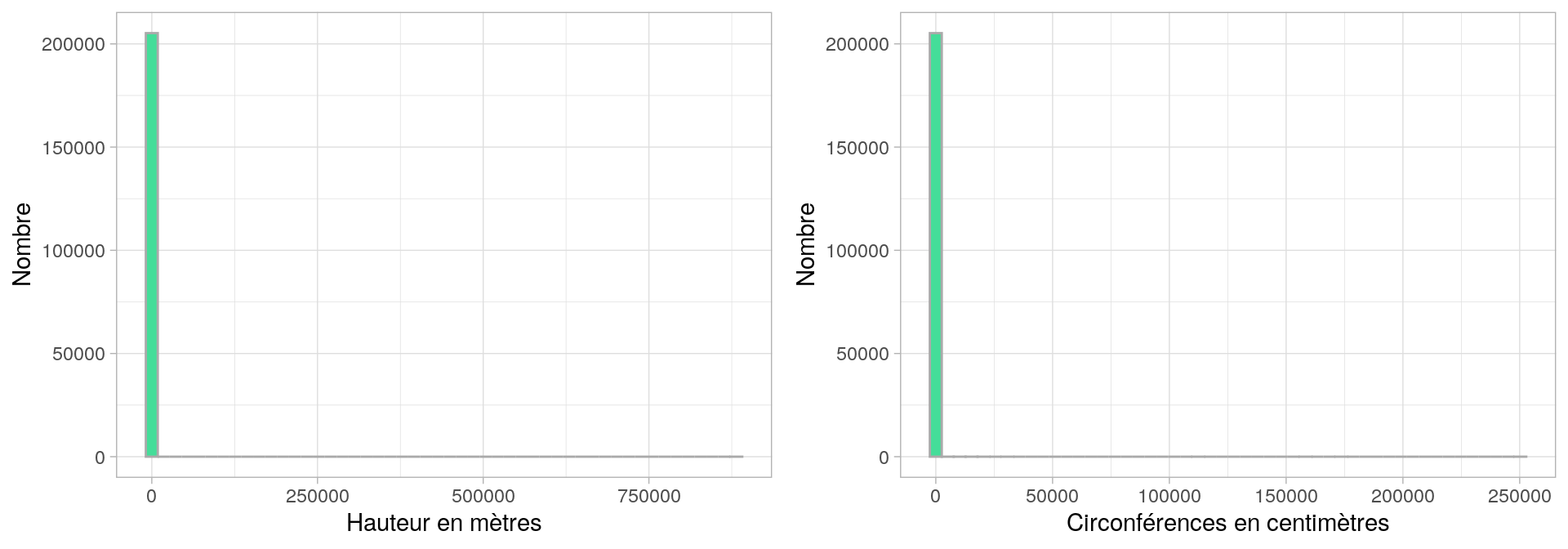
Données : arbres de la ville de Paris [https://opendata.paris.fr/]

Histogramme d'une distribution
réelle filtrée

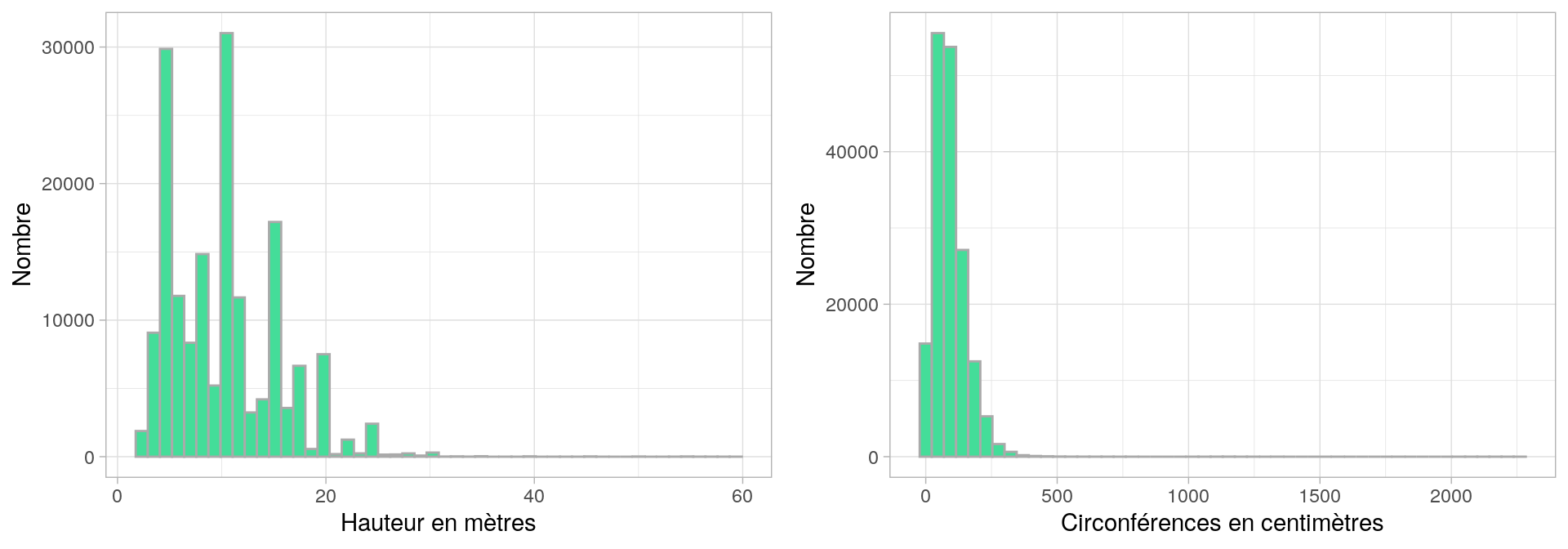
Données : arbres de la ville de Paris [https://opendata.paris.fr/]

Analyse univariée : plan

Objectif : Décrire la répartition des valeurs d’une variable

Mesures de tendance centrale

mode, moyenne, médiane

Mesures de dispersion

étendue, écart-type, variance, quantiles, coefficient de variation

Mesures de forme

symétrie (Skewness) et aplatissement (Kurtosis)

Statistique Descriptive
Univariée : la tendance

Moyenne(s), mode, médiane

Moyenne

$\displaystyle \bar{x} = \frac{1}{n}\sum_{i=0}^{n} x_i$

Moyenne pondérée

Lorsque les valeurs n'ont pas le même poids

Par exemple : poids = effectif de la valeur dans la population.

$\displaystyle \bar{x} = \frac{1}{\sum_{i=0}^{n} p_i}\sum_{i=0}^{n} p_i x_i$

Avantages et inconvénients
de la moyenne

Avantage

Chaque valeur compte

inconvénients

sensibilité aux valeurs extrêmes
pas de signification sur les valeurs discrètes (e.g. 2.5 enfants par femme)

exclure les outliers
utiliser un autre estimateur
étudier la distribution des valeurs (e.g. cas bimodal) et opérer une classification

Autres Moyennes

Moyenne géométrique

$\displaystyle \bar{x} = \sqrt[n]{\prod _{i=0}^{n} x_i}$

Moins sensible à la présence de valeurs extrêmes

Moyenne quadratique (RMS)

$\displaystyle \bar{x} = \sqrt{\frac{1}{n}\sum_{i=0}^{n} x_i^2}$

Cas particulier : Moyenne glissante

Moyenne calculée sur une fenètre de n valeurs consécutives.

e.g. on reçoit une mesure chaque seconde, très bruitée, et on désire afficher 10 minutes de signal lissé dans le temps

→ on calcule pour chaque point du signal, la moyenne sur 10 valeurs consécutives (5 en avant , 5 en arrière)

Le Mode

Mode : valeur la plus fréquente (effectif max.) de la série de valeurs que prend une variable.

⚠ si variable quantitative continue : faire une classification . Dans ce cas, le mode est la moyenne des valeurs min et max des bornes de la classe de plus grand effectif.

Avantages et inconvénients du mode

Avantages

Peu sensible aux valeurs extrêmes (moins sensible que la moyenne)

Signification concrète : la situation la plus fréquente

inconvénients

Ne dépends pas de toutes les observations : la modification d’une seule valeur n’entraîne pas une modification du mode

La Médiane

Médiane : valeur qui partage une série de valeurs en deux sous-ensembles d'égal effectif.

Comme en géométrie, la médiane est la valeur de la variable qui est la plus proche de toutes les autres.

étapes de calcul

Ordonner les valeurs selon un ordre croissant.

Calculer le rang $i=\frac{n+1}{2}$.

Si n impair, la valeur médiane existe dans la série statistique.

Si n pair, la valeur médiane est entre deux valeurs, et est égale à la moyenne de ces 2 valeurs.

Avantages et inconvénients
de la médiane

Avantages

Souvent plus pertinente que la moyenne

Peu sensible aux valeurs extrêmes (moins sensible que la moyenne)

Signification concrète : divise en deux la distribution : un individu sur deux a une valeur inférieure ou supérieure à celle-ci

inconvénients

Ne dépends pas de toutes les observations : la modification d’une seule valeur n’entraîne pas une modification de la médiane

Quelle mesure choisir ?

Tout dépend de la distribution !

→ Toujours afficher l'histogramme ou la distribution de densité !

Le Mode est privilégié pour les valeurs nominales et si on désire consider "le cas le plus fréquent".

Distribution sans longue traîne ?
→ moyenne et médiane

Plusieurs modes dans la distribution ?
→ classification puis médiane / moyenne par classe

Distribution bimodale

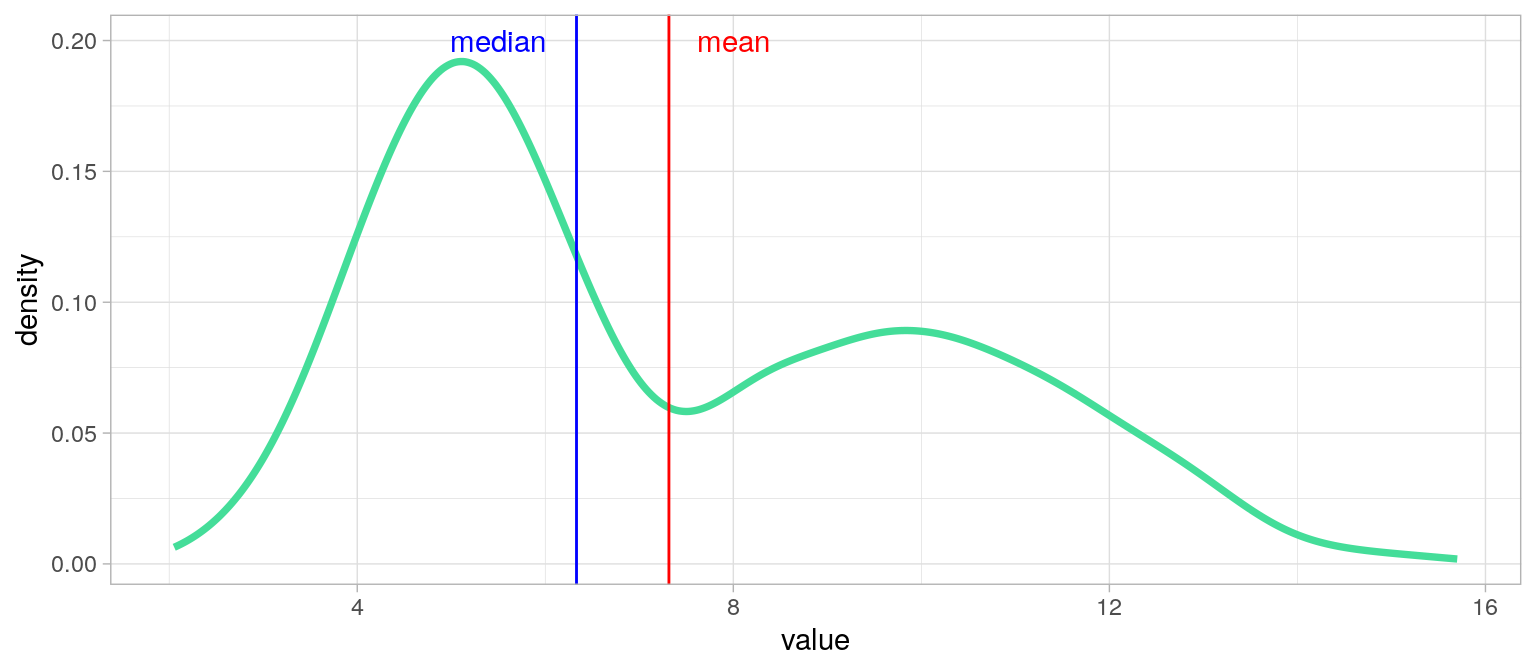
Que choisir : moyenne ou médiane ?

Distribution unimodale symétrique

from scipy.stats import gaussian_kde
xx = np.random.normal(loc=5, scale=1, size=2900)
density = gaussian_kde(xx) #kernel density estimator
x = np.linspace(min(xx), max(xx), 100)
y = density(x) #On estime la densité entre pour 100 valeurs entre xx_min et xx_max
plt.figure(figsize=(12, 5))
plt.plot(x, y, color="#44DD99", lw=1.3)
plt.axvline(x=np.mean(xx), color="red")
plt.axvline(x=np.median(xx) + 0.02, color="blue")
plt.text(4.5, 0.2, "mean", color="red")
plt.text(5.5, 0.2, "median", color="blue")
plt.xlabel("value")
plt.ylabel("density")
plt.grid(True)
plt.show()

xx = pd.Series(np.random.normal(loc=5, scale=1, size=2900))
ax = xx.plot(
	kind="density", ind=np.linspace(min(xx), max(xx), 100),
	figsize=(12, 5), color="#44DD99", lw=1.3, grid=True,
	xlabel="value", ylabel="density")
ax.axvline(x=xx.mean(), color="red")
ax.axvline(x=xx.median() + 0.02, color="blue")
ax.text(4.5, 0.2, "mean", color="red")
ax.text(5.5, 0.2, "median", color="blue")
ax.set_xlabel("value")

xx <- data.frame(value=rnorm(2900,mean = 5, sd = 1))
plot1 <- ggplot(xx)+
		geom_line(aes(x = value),stat = "density", color="#44DD99", lwd= 1.3)+
		geom_vline(xintercept = mean(xx$value), color="red")+
		geom_vline(xintercept = median(xx$value) + 0.02,color="blue")+
		annotate("text", x=c(4.5,5.5), y=c(0.2,0.2), colour=c("red","blue"),label=c("mean", "median"))+
		theme_light()
plot1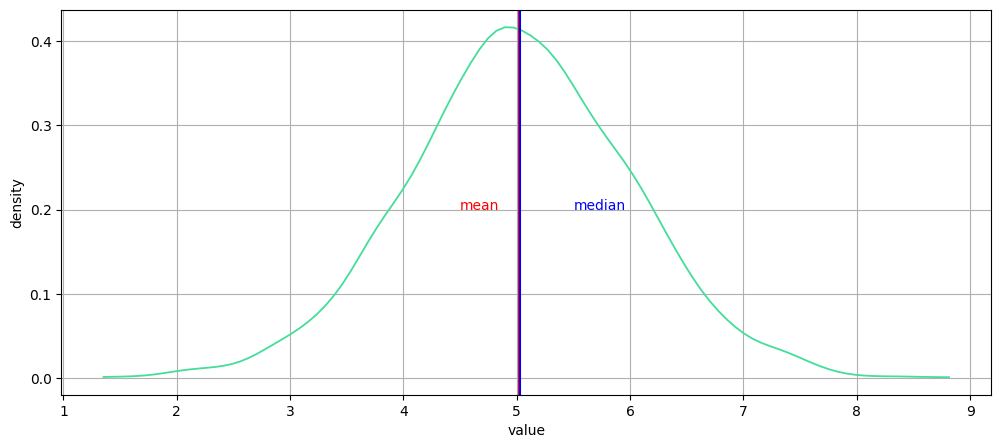

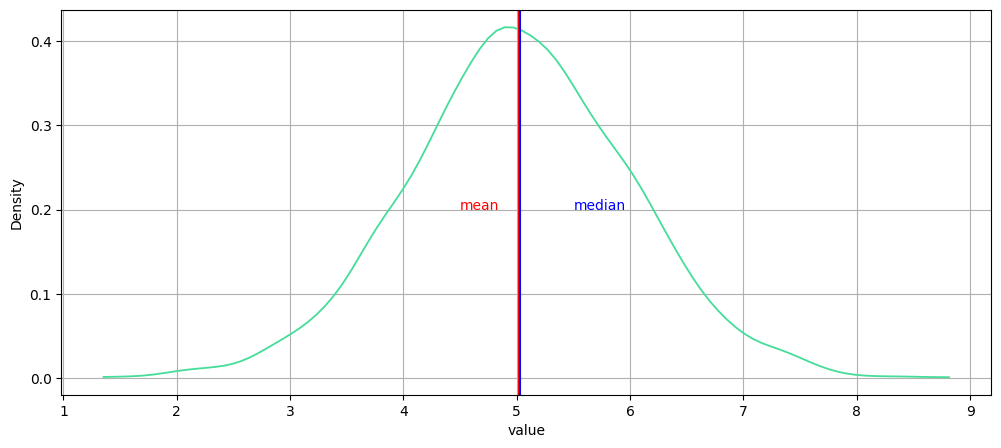
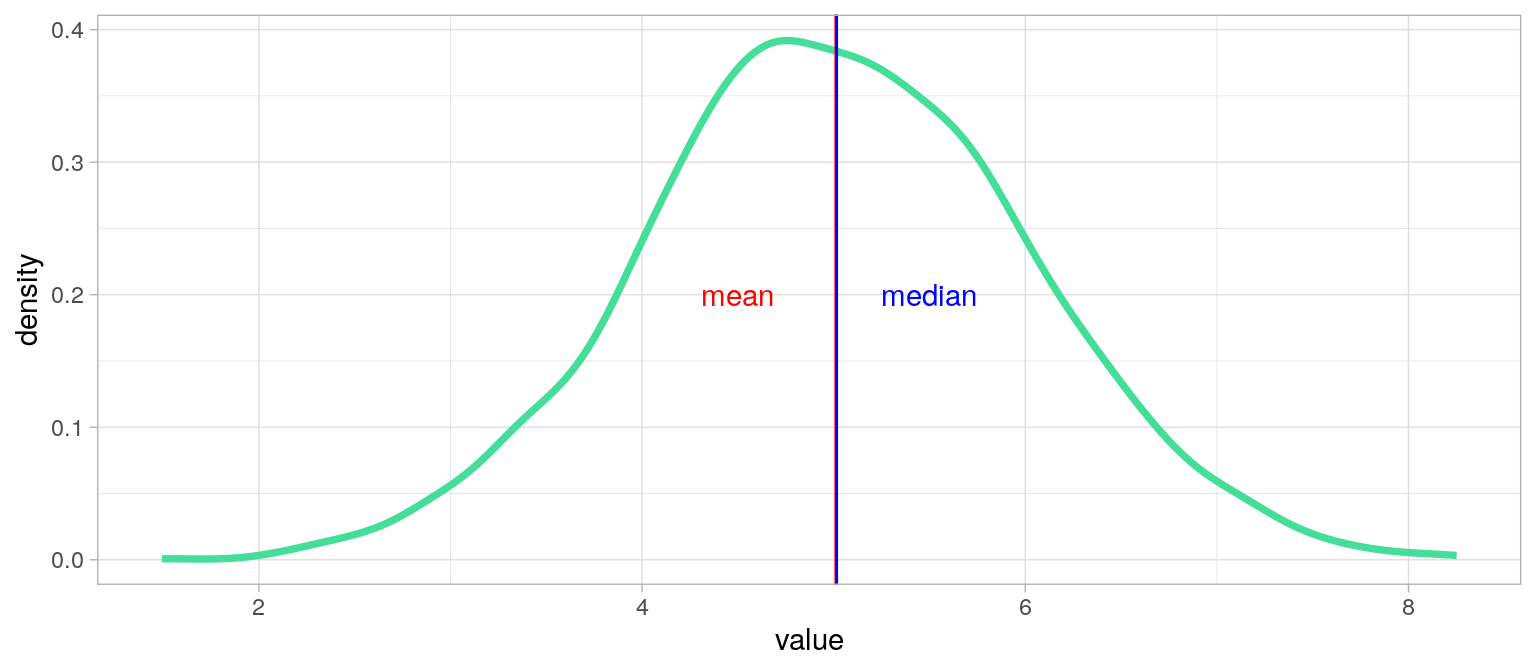
Histogramme et distribution

Histogramme pour un vecteur numérique :

plt.figure(figsize=(12, 3))
x = np.random.geometric(p=0.5, size=2500) #eg: Combien de fois lancer une pièce avant de tomber sur face
plt.hist(x, bins=10)
plt.title("Histogram of x")
plt.xlabel("x")
plt.ylabel("Frequency")
plt.show()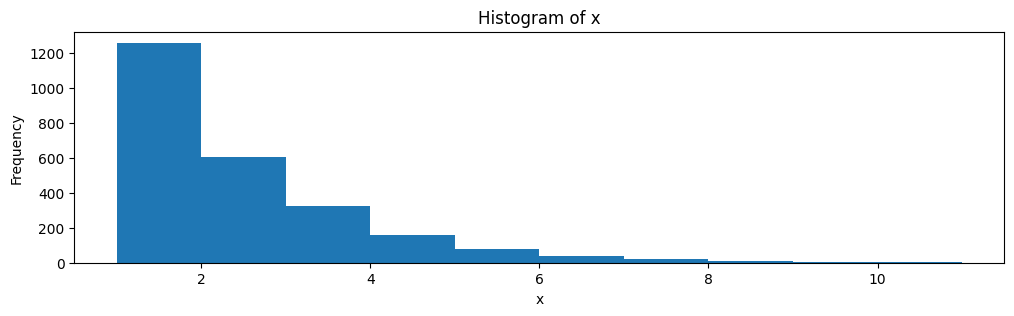

Histogramme et distribution

Un histogramme n’a pas de sens pour une variable qualitative.
On peut utiliser plt.bar, ⚠ mais ce n’est plus une distribution !

colors = sorted(["blue", "yellow", "red", "green", "purple", "orange", "black"])
samples = np.random.choice(colors, size=2500, replace=True)#['black', 'red', 'orange', ..., 'purple', 'green', 'purple']
plt.figure(figsize=(12, 3))
plt.bar(colors, np.unique(samples, return_counts=True)[1], color=colors)
plt.show()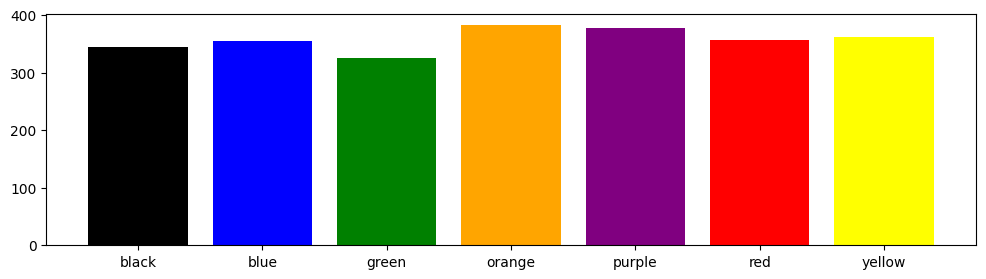

Statistique Descriptive
Univariée : la dispersion

Variance, écart-type, Coeff. de variation.

La dispersion statistique

xy = np.random.normal(size=(900, 900))
plt.figure(figsize=(5, 5))
plt.scatter(xy[:, 0], xy[:, 1], s=21, color="#44DD99", edgecolor="#666666")
plt.xlabel("X")
plt.ylabel("Y")
plt.grid(True)
plt.axis("equal")
plt.show()

xy = pd.DataFrame(np.random.normal(size=(900, 900)))
xy.plot(kind="scatter", x=0, y=1, s=[21], color="#44DD99", edgecolor="#666666", figsize=(5, 5), grid=True)
plt.xlabel("X")
plt.ylabel("Y")
plt.axis("equal")
plt.show()

mydataset <- data.frame(X=rnorm(900), Y=rnorm(900))
plot1 <- ggplot(mydataset)+
		geom_point(aes(x=X, y=Y), fill="#44DD99", color="#666666", shape=21)+
		coord_equal()+theme_light()
plot1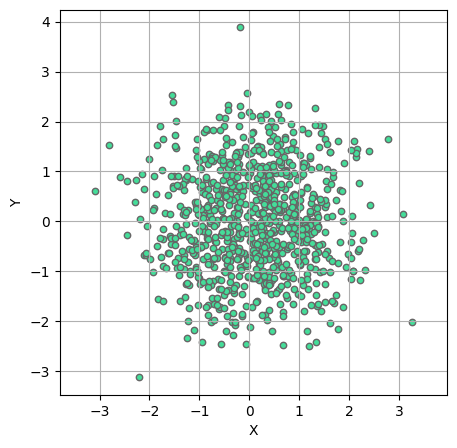

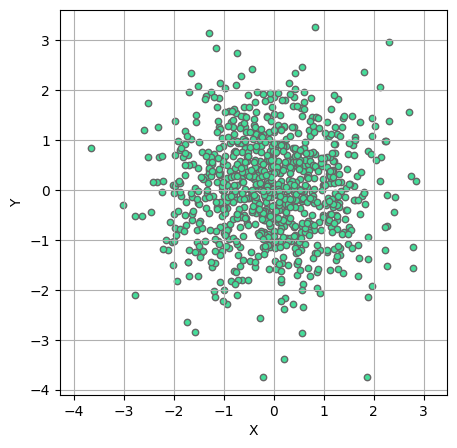
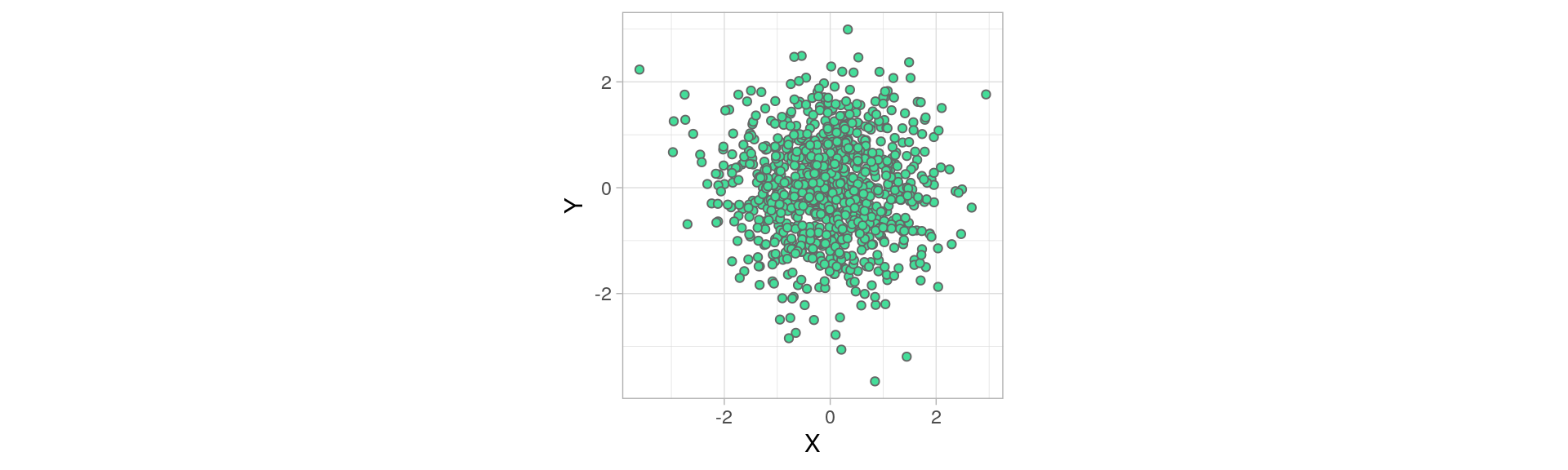
Variance et écart-type

La variance est la somme des écarts carrés à la moyenne rapporté à l’effectif.

$\displaystyle var_x = \frac{1}{n}\sum_{i=0}^{n} (x_i -\bar{x})^2$

Avec $X$ une variable, $x_i$ les valeurs de la variable, $\bar{x}$ la moyenne de $X$, et $n$ l'effectif.

$\sigma_x = \sqrt{var_x}$ : l'écart type est la racine carrée de la variance.

Même moyenne et variances différentes

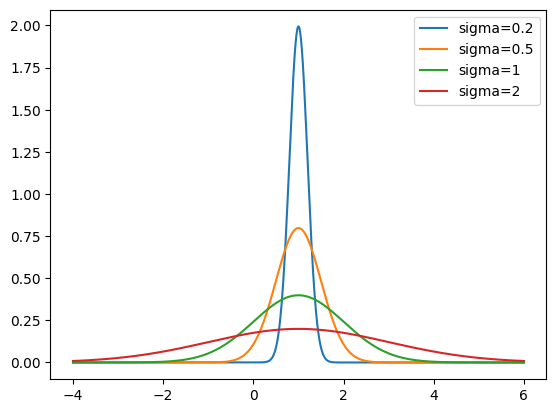
Variance et écart-type

Variance et écart-type rendent compte de la dispersion de la variable autour de sa moyenne.

Ils sont sensibles aux valeurs extrêmes et toujours positifs.

Si $var_X=0$ ou $\sigma_x=0$ , alors X est constante.

Un écart-type faible indique que les valeurs sont réparties de façon homogène autour de la moyenne.

Lorsque $X \sim \mathcal{N}(\mu, \sigma)$

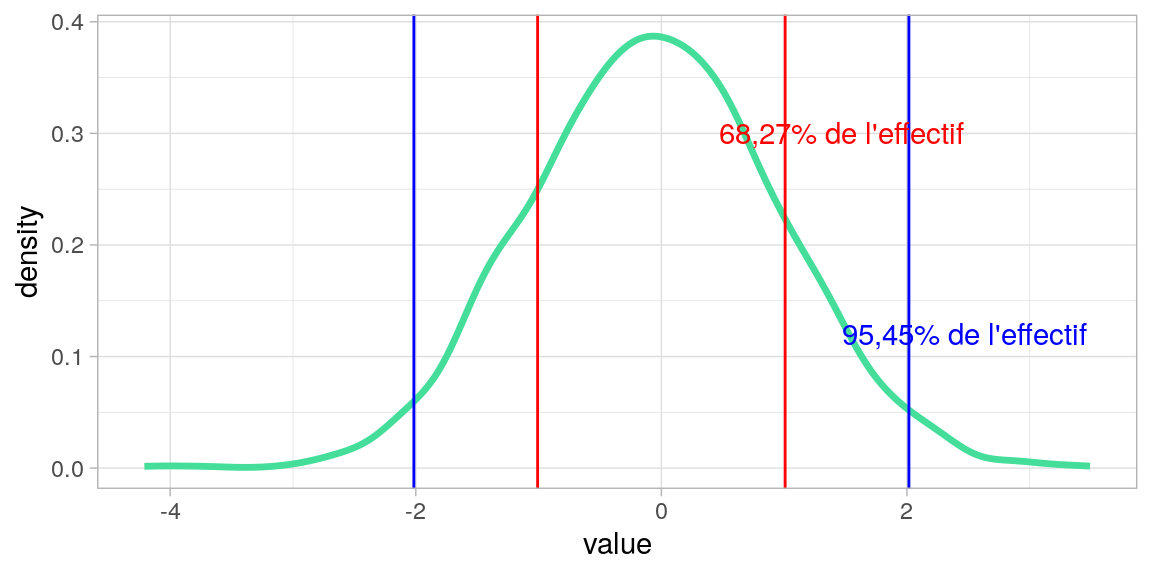
$[\mu - \sigma ; \mu+\sigma] \approx \frac{2}{3}$ de l'effectif.
$[\mu - 2\sigma ; \mu+2\sigma] \approx 95\%$ de l'effectif.
$[\mu - 3\sigma ; \mu+3\sigma] \approx 99\%$ de l'effectif.

Quantiles

La médiane sépare une population en deux classes d'égal effectif selon la valeur d'une variable (quantitative).

Les quantiles séparent une population en n classes d'égal effectif.

Les quartiles d'une population selon une variable $X$ sont trois valeurs $Q_1, Q_2, Q_3$,qui séparent une population en quatres classes d'égal effectif.

25% des valeurs de $X$ sont strictement inférieures à $Q_1$
50% des valeurs de $X$ sont strictement inférieures à $Q_2$ (médiane)
75% des valeurs de $X$ sont strictement inférieures à $Q_3$

De même, déciles et centiles.

écarts inter-quartiles et inter-déciles

Deux mesures de la dispersion d’une distribution :

Écart inter-quartile: $Q_3-Q_1$, capture 50% des valeurs de la population les plus proches de la médiane.

Écart inter-décile: $Q_9-Q_1$, capture 80% des valeurs de la population les plus proches de la médiane.

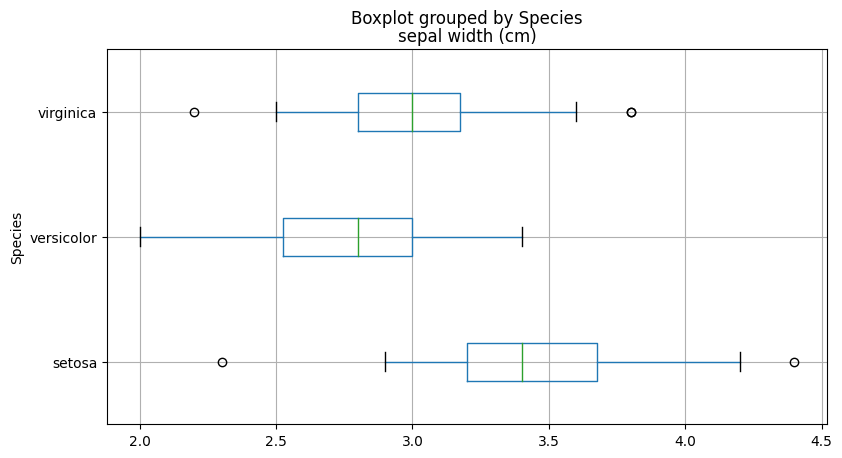
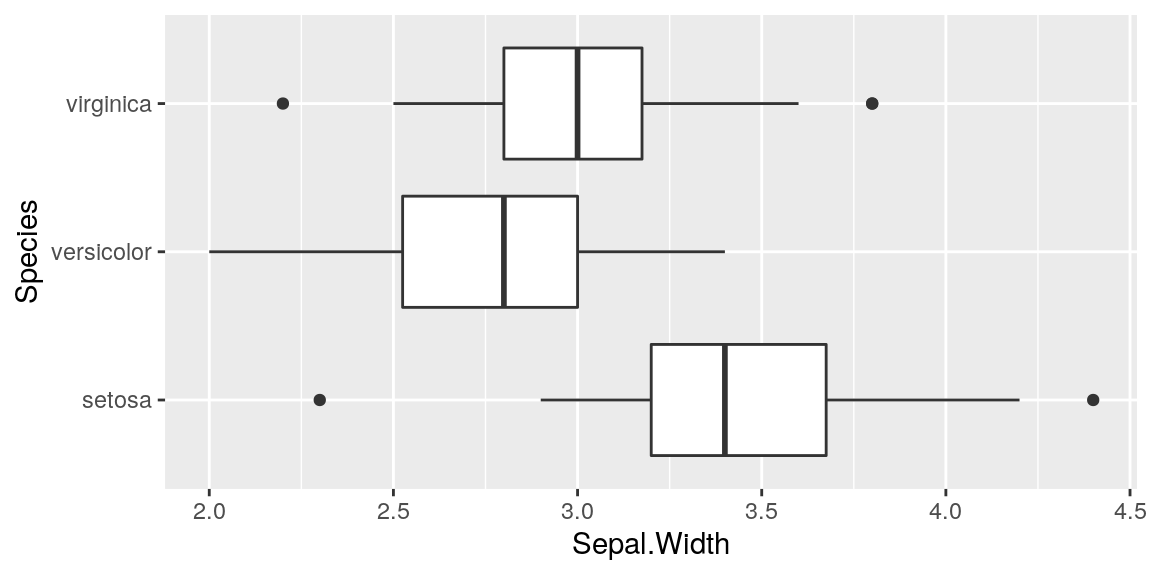
Les boîtes à moustaches (boxplots)

Représentation courante de la dispersion d’une variable à l’aide de quartiles

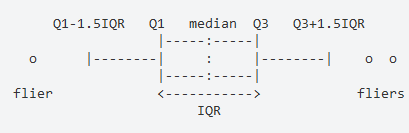
La marque centrale de la boîte est la médiane
Les bords de la boîte sont les quartiles $Q_1$ et $Q_3$
Les extrémités des moustaches vont jusqu’à la plus grande (resp. la plus petite ) valeur inférieure (resp. supérieure) à 1.5 fois l’écart interquartile
Les valeurs qui dépassent les moustaches sont affichées sous formes de points.

Les boîtes à moustaches (boxplots)

from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['Species'] = iris.target_names[iris.target]
df.boxplot(by='Species', column='sepal width (cm)', vert=False, figsize=(9, 5))
plt.show()

from sklearn.datasets import load_iris
iris = load_iris()
#We create a list by species of sepal widths.
x = [iris.data[iris.target==i, 1] for i in np.unique(iris.target)]
plt.figure(figsize=(9, 5))
plt.boxplot(x, labels=iris.target_names, vert=False)
plt.grid()
plt.xlabel("sepal width (cm)")
plt.ylabel("Species")
plt.show()

plot1 <- ggplot(iris)+
geom_boxplot(aes(y=Sepal.Width,x= Species) ) + coord_flip()
plot1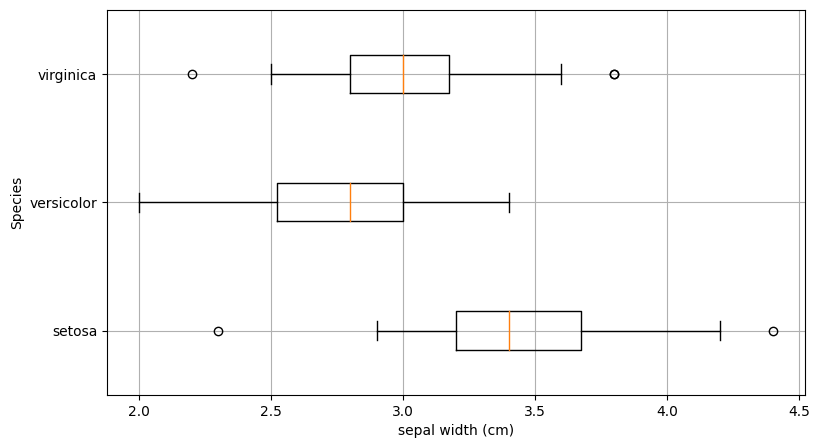

Avantages et inconvénients
des quantiles

Avantages

Peu sensibles aux distributions aplaties et aux valeurs extrêmes

L’écart inter-quantile est plus robuste que l’écart-type

inconvénients

Parfois délicat pour les variables quantitatives discrètes

Les écarts inter-quantiles négligent l’influence des valeurs extrêmes sur la distribution

Le coefficient de variation

Le coefficient de variation (CV) est une autre mesure de dispersion.

C'est le ratio entre l'écart-type $\sigma_x$ et la moyenne $\bar{x}$ d'une variable quantitative X.

$CV(X)=\frac{\sigma_x}{\bar{x}}$

Plus il est important, plus la dispersion est grande.

Plus il est proche de 0, plus les données sont homogènes.

Il souffre des mêmes inconvénients que la moyenne et l'écart-type : sensibilité aux valeurs extrêmes.

Comparaison de dispersion de deux distributions de valeurs

Exemple : deux communes versent des aides aux entreprises locales.

Commune A : moyenne = 390€, $\sigma$ = 30€

Commune B : moyenne = 152€, $\sigma$ = 8€

Pour quelle commune les aides sont les plus homogènes ?

On pourrait aussi comparer des distribution de valeurs exprimées dans des unités différentes !

(Mauvaise) Comparaison visuelle de deux distributions

A = np.random.normal(size=10000, loc=390, scale=30)
B = np.random.normal(size=10000, loc=152, scale=8)
plt.figure(figsize=(20, 3))
ax = plt.subplot(1, 2, 1)
plt.hist(A, bins=10, color="white", edgecolor="black", density=True)
ax.set_xlabel("A")
ax.set_ylabel("Density")
ax.set_title("Histogram of A")
ax = plt.subplot(1, 2, 2)
plt.hist(B, bins=10, color="white", edgecolor="black", density=True)
ax.set_xlabel("B")
ax.set_ylabel("Density")
ax.set_title("Histogram of B")
plt.show()

A <-  rnorm(n = 10000, mean = 390, sd = 30)
B <-  rnorm(n = 10000, mean = 152, sd = 8)
par(mfrow=c(1, 2)) #2 graphes en colonnes
hist(A, probability = T)
lines(density(A), col="red")
hist(B, probability = T)
lines(density(B), col="red")

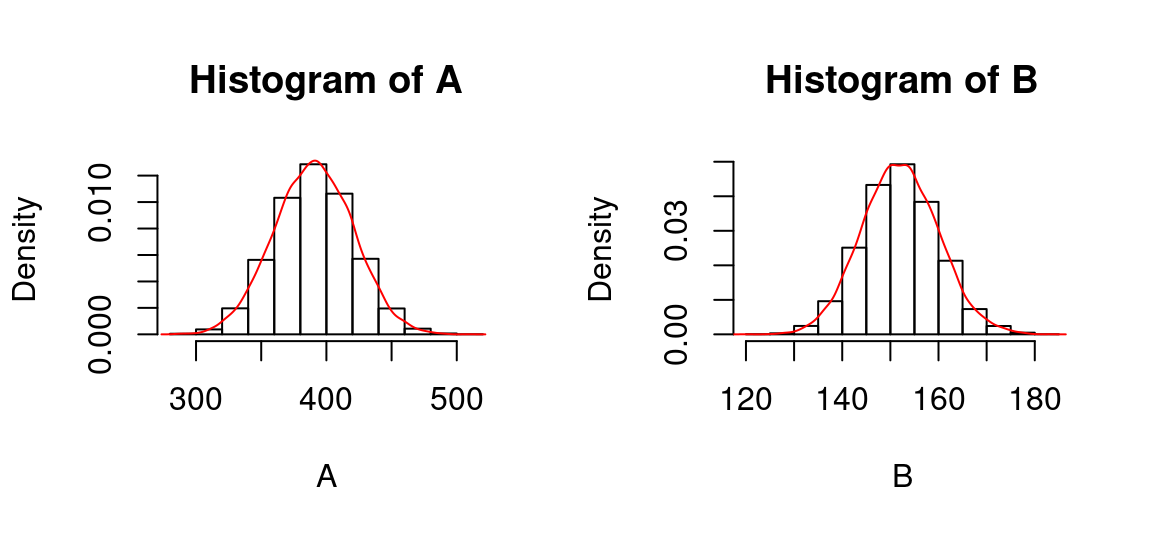
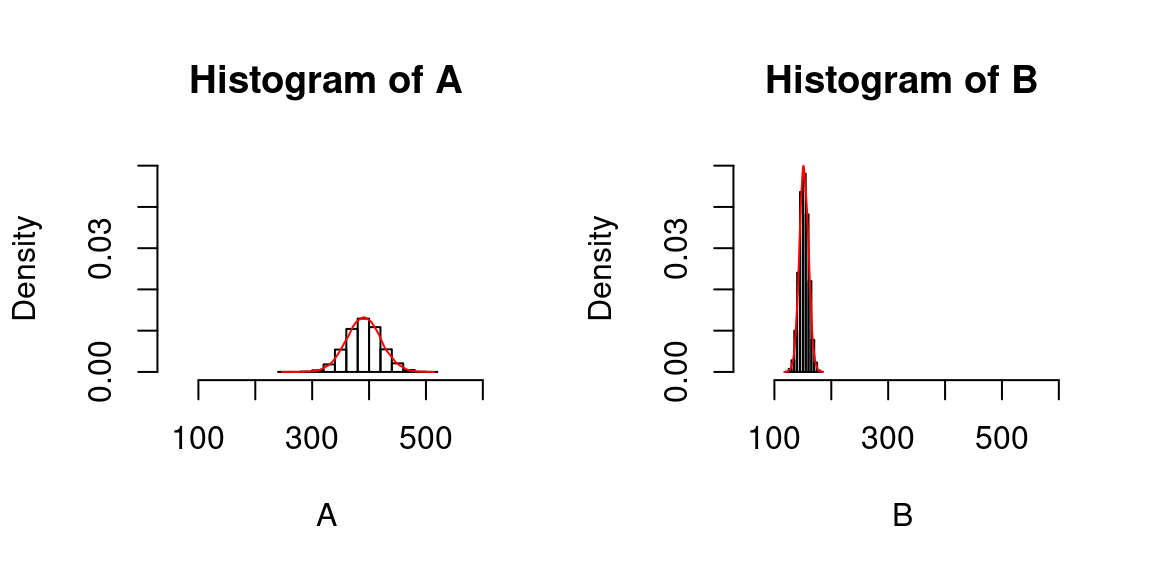
Qu'est-ce qui ne va pas ?

Comparaison visuelle de deux distributions

Il faut une échelle commune !

A = np.random.normal(size=10000, loc=390, scale=30)
B = np.random.normal(size=10000, loc=152, scale=8)
plt.figure(figsize=(20, 3))
ax1 = plt.subplot(1, 2, 1)
plt.hist(A, bins=10, color="white", edgecolor="black", density=True)
ax1.set_xlabel("A")
ax1.set_ylabel("Density")
ax1.set_title("Histogram of A")
ax2 = plt.subplot(1, 2, 2, sharex=ax1, sharey=ax2)
plt.hist(B, bins=10, color="white", edgecolor="black", density=True)
ax.set_xlabel("B")
ax.set_ylabel("Density")
ax.set_title("Histogram of B")
plt.show()

A <-  rnorm(n = 10000, mean = 390, sd = 30)
B <-  rnorm(n = 10000, mean = 152, sd = 8)
par(mfrow=c(1, 2))
hist(A, probability = T, xlim = c(50,600), ylim = c(0,0.05))
lines(density(A), col="red")
hist(B, probability = T,xlim = c(50,600), ylim = c(0,0.05))
lines(density(B), col="red")

Statistique Descriptive
Univariée : la forme

Symétrie, applatissement

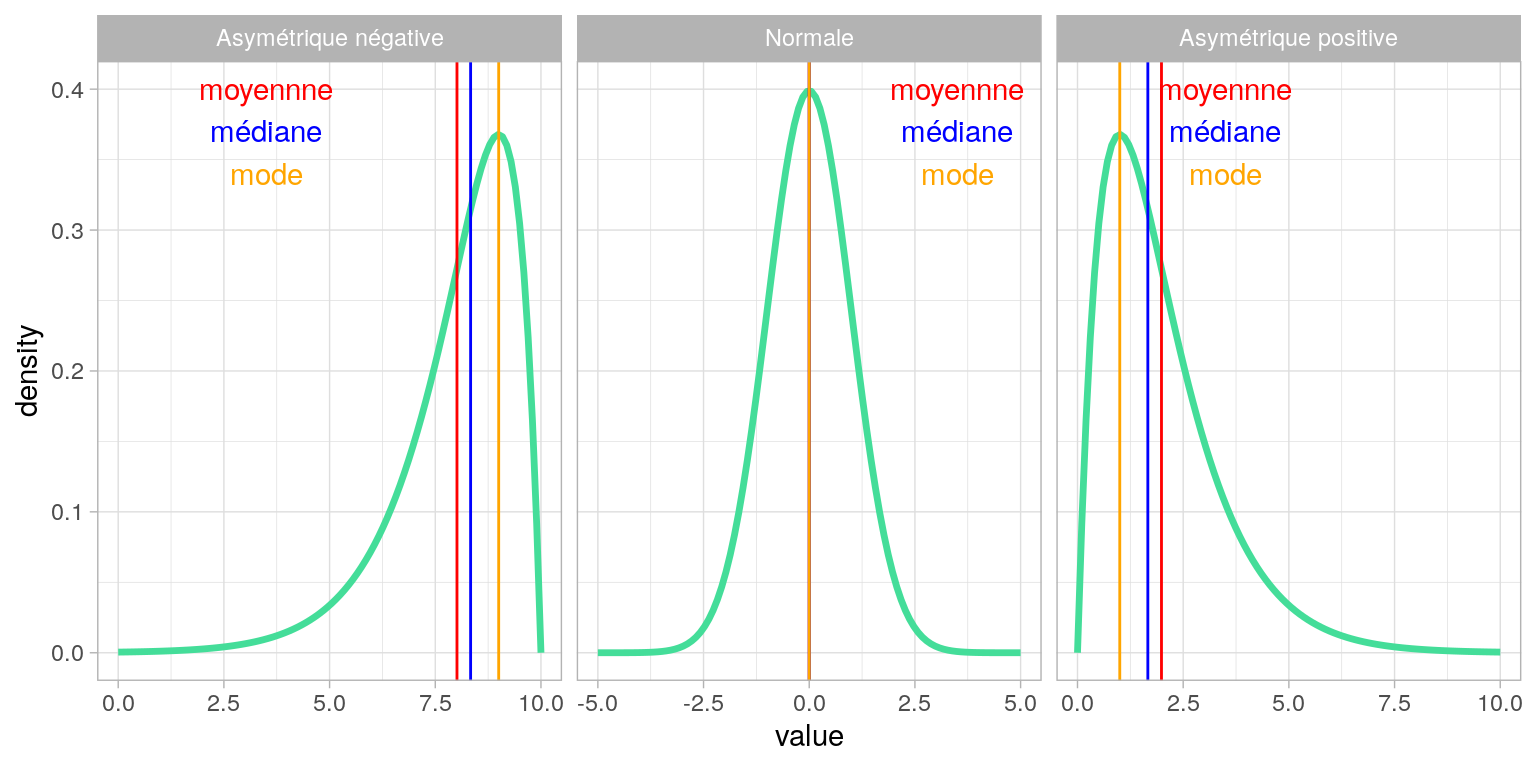
Asymétrie des distributions

Les coefficients de Pearson

Deux moyens simples d'estimer l'asymétrie

$C_1 = \frac{\bar{x} - mode(X)}{\sigma_x}$

$C_2 = \frac{3(\bar{x} - mediane(X))}{\sigma_x}$

Interprétation des coefficients d’asymétrie

Si le coefficient est nul, la distribution est symétrique.
Si le coefficient est négatif, la distribution est déformée à gauche de la médiane (sur-représentation de valeurs faibles, à gauche)
Si le coefficient est positif, la distribution est déformée à droite de la médiane (sur-représentation de valeurs fortes, à droite)

Le coefficient de Fischer

Ce coefficient est le moment d’ordre 3 de la variable $X$ ( de moyenne $\mu$ et d’écart-type $\sigma$) centrée réduite

$skewness = \mathbb{E} \left[ \left( \frac{X - \mu}{\sigma} \right)^3 \right] = \frac{\Sigma_{i=0}^n(x_i - \bar{x})^3}{n\sigma^3}$

L'applatissement des distributions (Kurtosis)

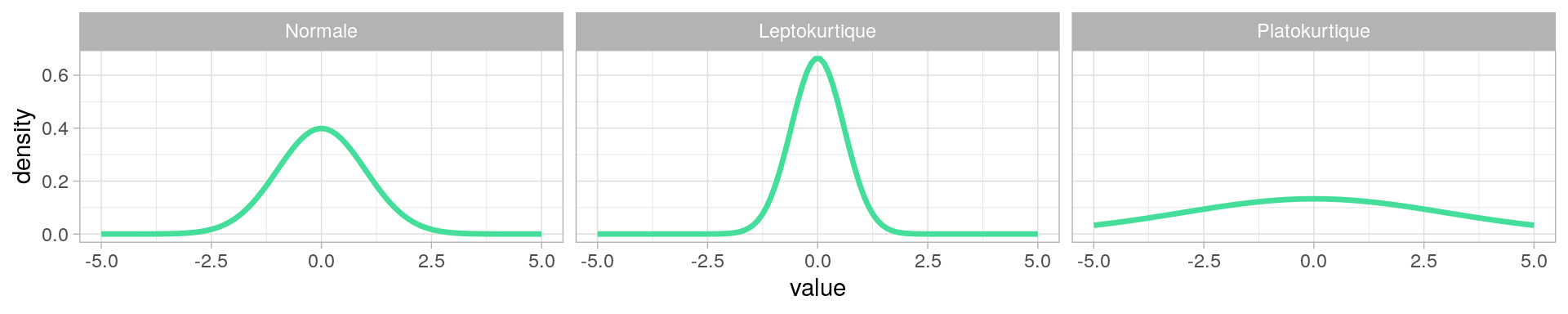
Courbe piquée: Peu de variation, distribution relativement homogène, beaucoup de valeurs égales ou proches de la moyenne.

Courbe applatie: Variations importantes, distribution relativement hétérogène, beaucoup de valeurs s’éloignent de la moyenne.

Coefficient d'applatissement : Kurtosis

Coefficient non normalisé :

$K=\frac{\Sigma_{i=0}^n(x_i - \bar{x})^4}{n\sigma^4}$

Si la distribution est normale, $K=3$

Si $K>3$, la distribution est plus applatie.

Si $K<3$, la distribution est moins applatie.

On normalise parfois en considérant $K′=K−3$ (excès d’applatissement)

Représentation d’une distribution et Échelle de couleurs

Distribution et Échelle de couleurs

Pour une variable quantitative continue qu’on souhaite colorer, il n’est pas toujours possible de graduer une échelle de couleur continue.

Il faut (souvent) classer les valeurs en catégories. Le nombre de classes et les méthodes de classification varient.

En général : 5, 7 ou 9 classes

< 5 trop peu de détails
> 9 difficile de distinguer les classes proches

Distribution et Échelle de couleurs

Méthodes de classifications de Qgis

Ruptures Naturelles (Jenks) : Minimisation des variances intra-classe et maximisation des variances inter-classe
Effectifs égaux (quantiles)
Intervalles égaux
Ecart-type : intervales de 1 ou 0.5 σ
Jolies ruptures : intervalle égaux “décalés” pour faire joli : nombre ronds, puissances de 10…

Exemple avec la surface des quartiers de Paris

import geopandas as gpd
quartier = gpd.read_file("quartier_paris.shp")
quartier.plot(figsize=(15, 5), edgecolor="black")

quartiers <-  st_read("quartier_paris.shp")
plot(quartiers$geometry)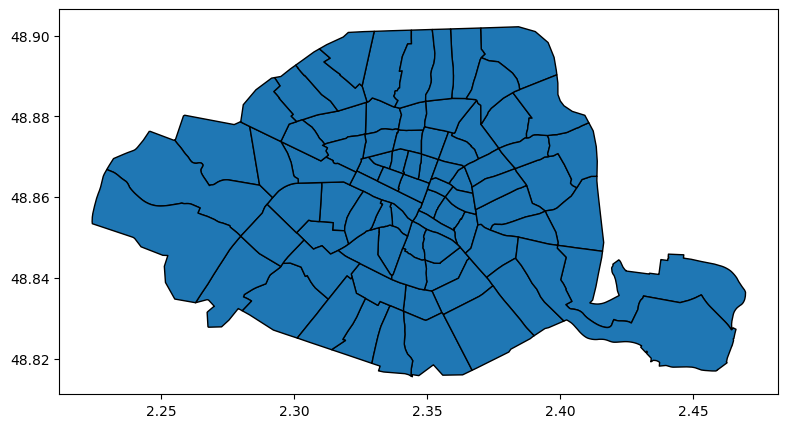

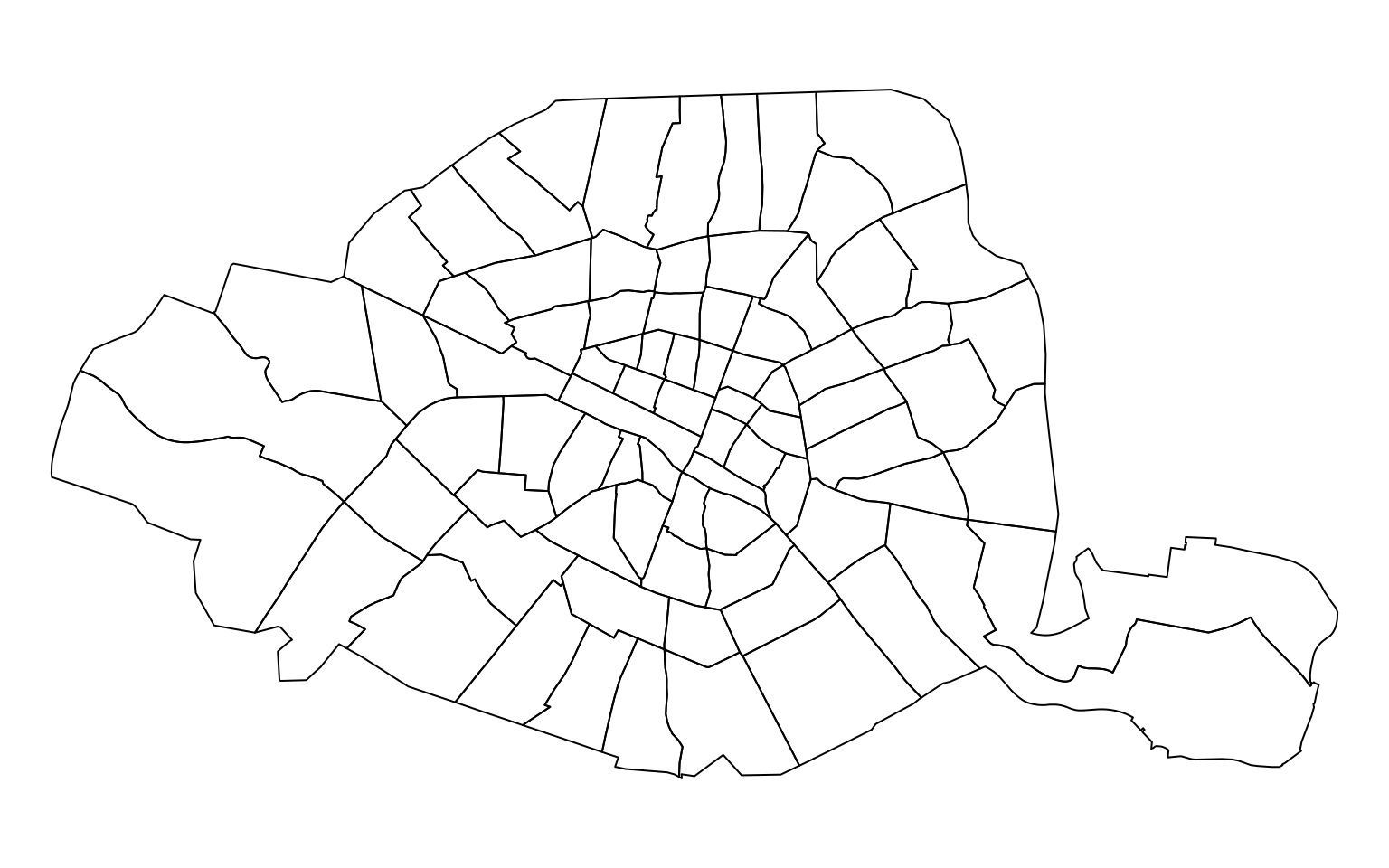
Allure de la distribution

quartier["surface"].plot(
	kind="hist", bins=15, xlabel="surface [m²]", ylabel="count",
	figsize=(15, 5), title="Histogram of surface")

hist(quartiers$surface,breaks = 15)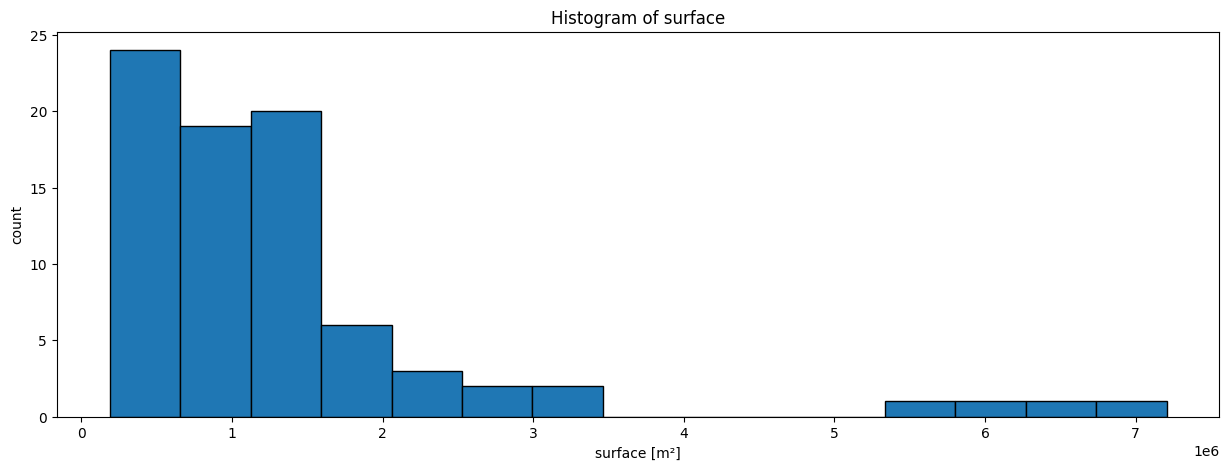

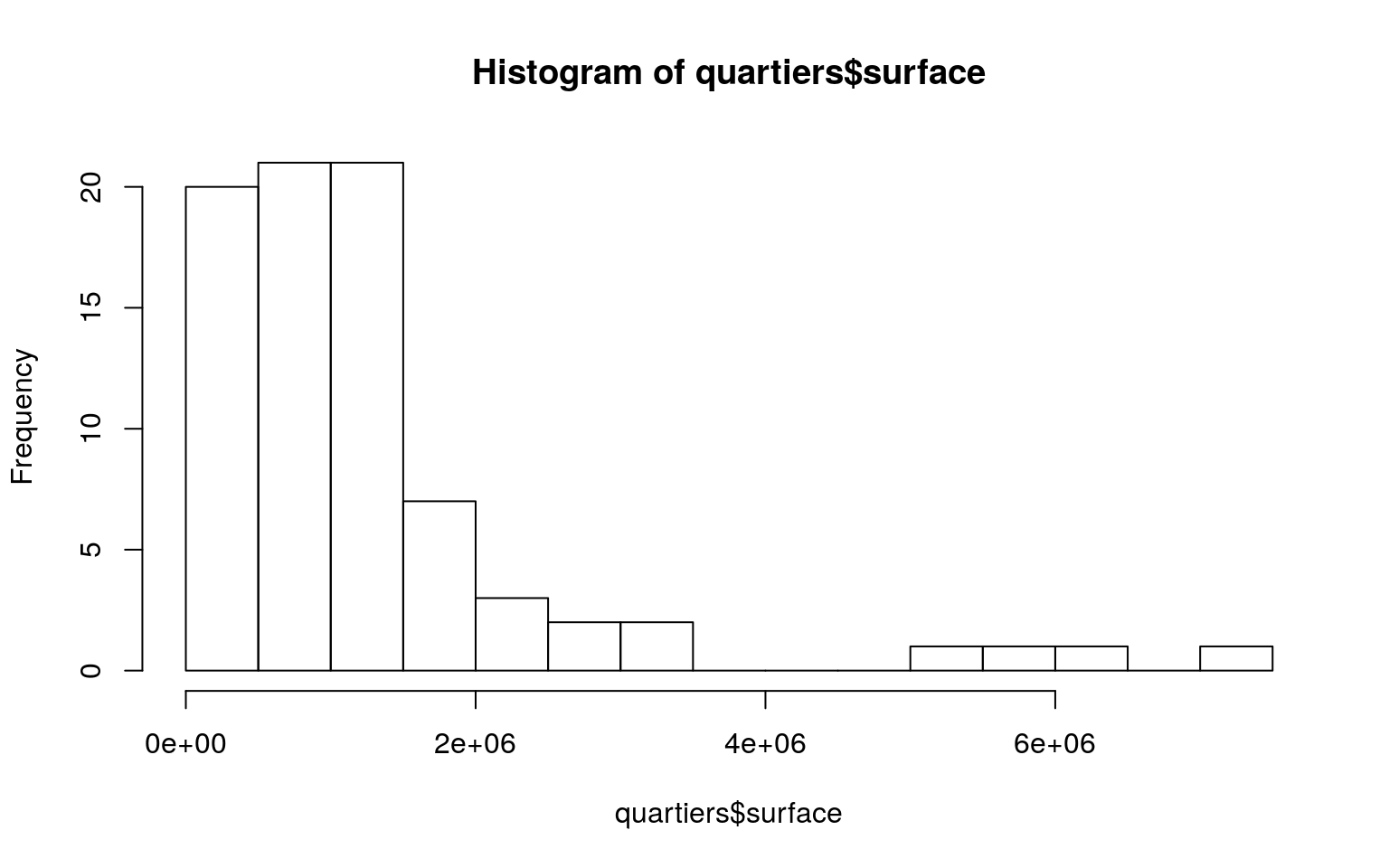
Affichage par défaut :

quartier.plot(column="surface", legend=True, figsize=(15, 5), edgecolor="black").set_title("Surface")

par(mar=c(0,0,0,0))
plot(quartiers["surface"])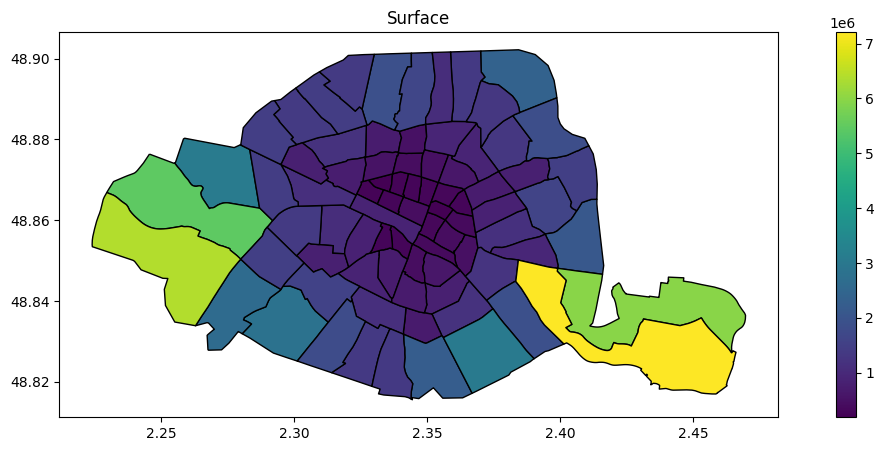

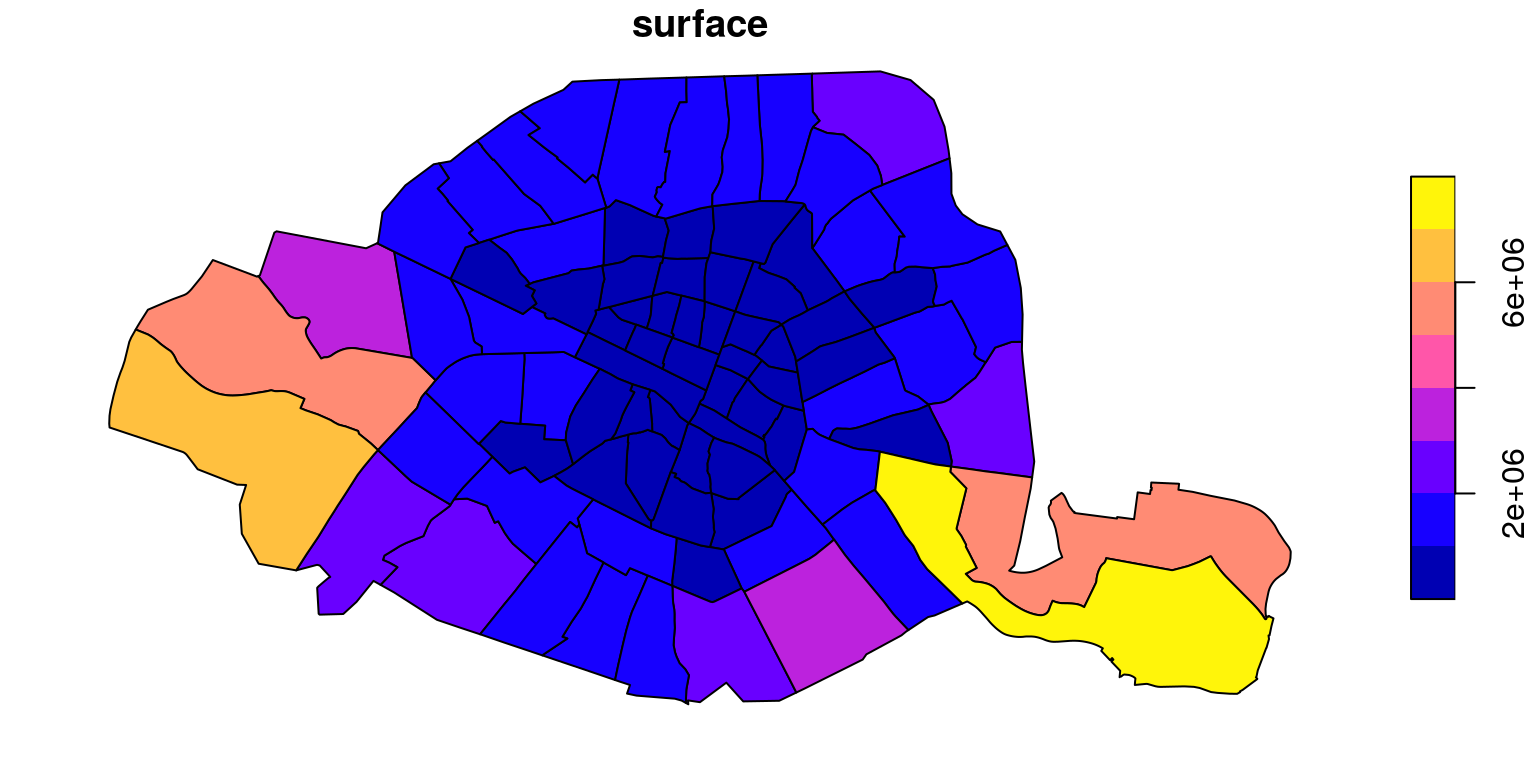
Par défaut la fonction plot de sf utilise la méthode “pretty” avec 10 ruptures (9±1 classes) => ce sont des intervalles égaux.

Par défaut la fonction plot de géopandas utilise une échelle continue.

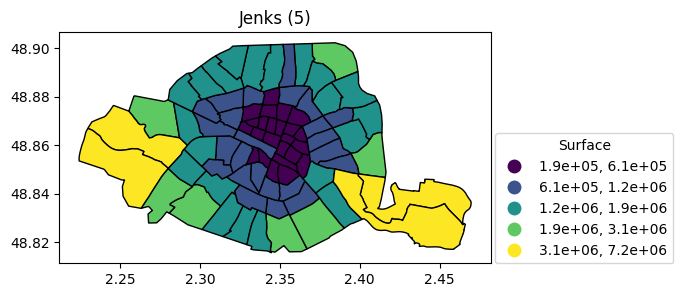
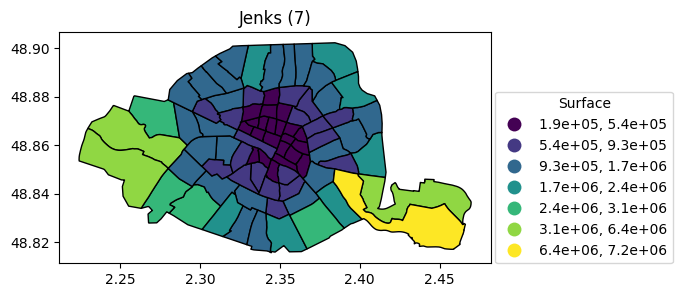
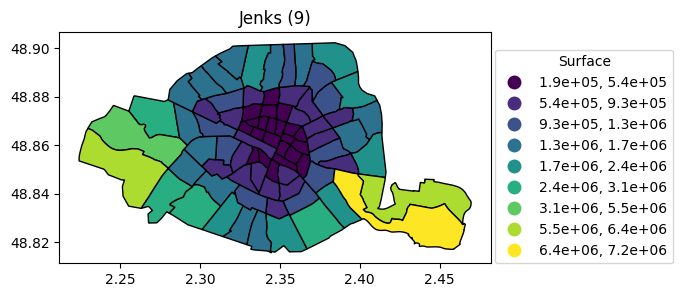
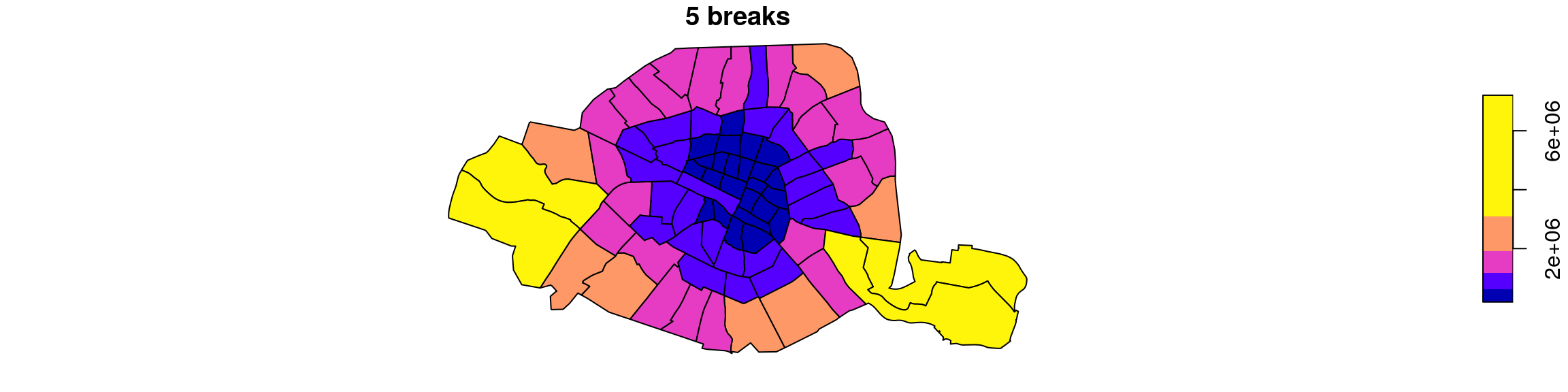
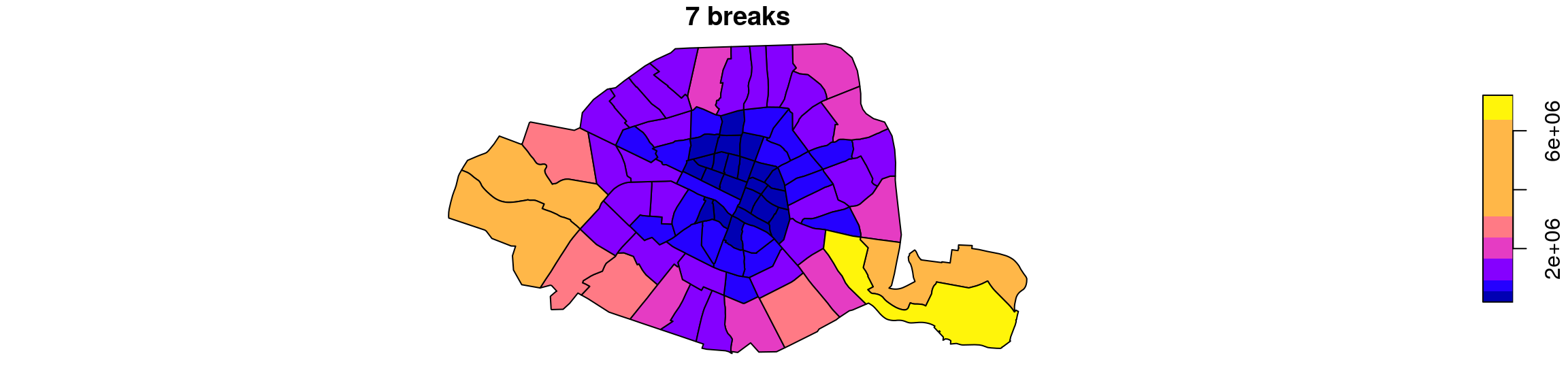
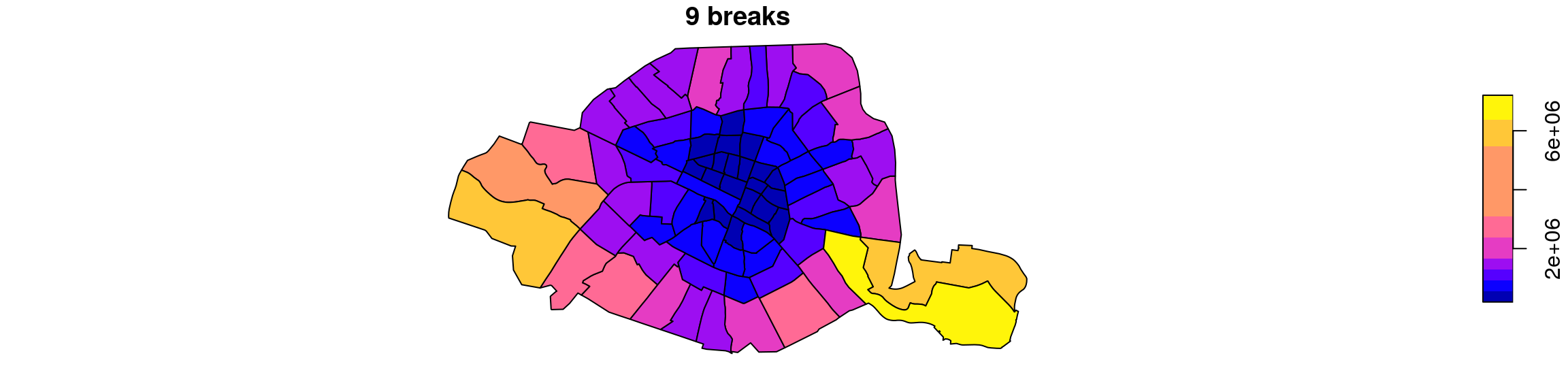
Jenks à 5 , 7 et 9 classes

Code R correspondant :

Code Python correspondant :

import mapclassify
quartier.plot(
	column="surface", scheme="naturalbreaks", k=5, legend=True, figsize=(15, 3), edgecolor="black",
	legend_kwds={"title": "Surface", "loc": (1.01, 0), "fmt": "{:.1e}"}).set_title("Jenks (5)")

quartier.plot(
	column="surface", scheme="naturalbreaks", k=7, legend=True, figsize=(15, 3), edgecolor="black",
	legend_kwds={"title": "Surface", "loc": (1.01, 0), "fmt": "{:.1e}"}).set_title("Jenks (7)")

quartier.plot(
	column="surface", scheme="naturalbreaks", k=9, legend=True, figsize=(15, 3), edgecolor="black",
	legend_kwds={"title": "Surface", "loc": (1.01, 0), "fmt": "{:.1e}"}).set_title("Jenks (9)")

par(mar=c(0,0,0,0))
plot(quartiers["surface"], breaks="jenks", nbreaks = 5, main = "5 breaks")
plot(quartiers["surface"], breaks="jenks", nbreaks = 7, main="7 breaks")
plot(quartiers["surface"], breaks="jenks", nbreaks = 9, main= "9 breaks")

Effectifs égaux (quantiles)

ax = quartier.plot(
	column="surface", scheme="quantiles", k=5, legend=True, figsize=(15, 5), edgecolor="black",
	legend_kwds={"title": "Surface", "loc": (1.01, 0), "fmt": "{:.1e}"}
	)
ax.set_title("Effectifs égaux")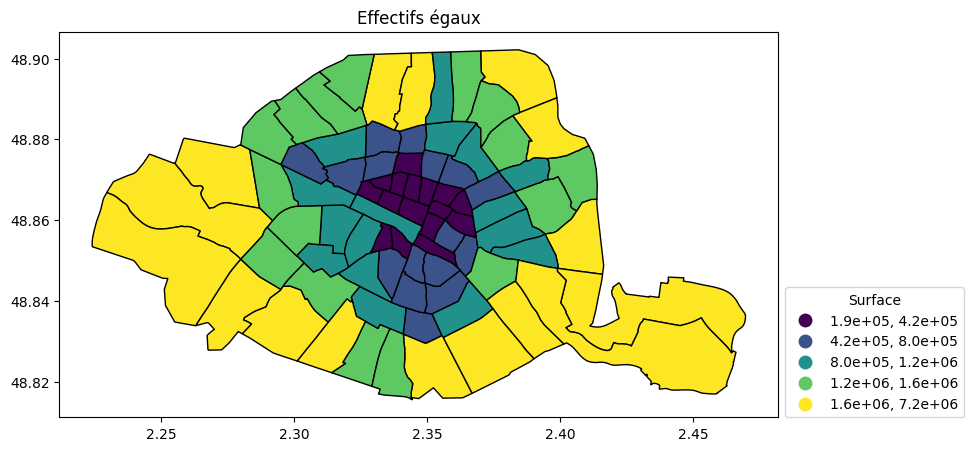

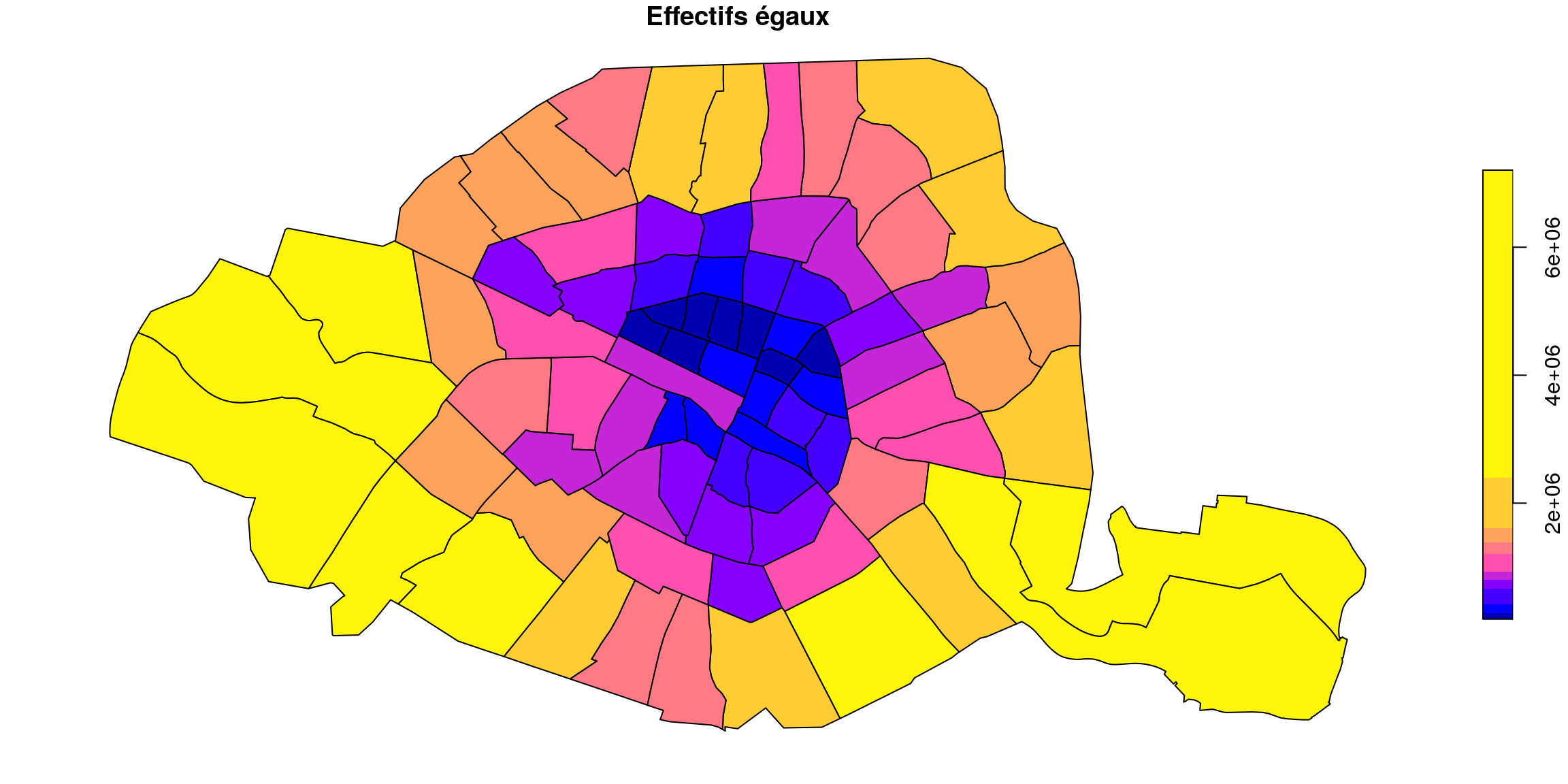
Intervalles égaux (7)

quartier.plot(
	column="surface", scheme="equal_interval", k=7, legend=True,
	legend_kwds={"title": "Surface", "loc": (1.01, 0), "fmt": "{:.2e}"}, figsize=(15, 5), edgecolor="black"
	).set_title("Intervalles égaux (7)")

par(mar=c(0,0,0,0))
plot(quartiers["surface"], breaks="equal", nbreaks = 7, main = "Intervalles égaux")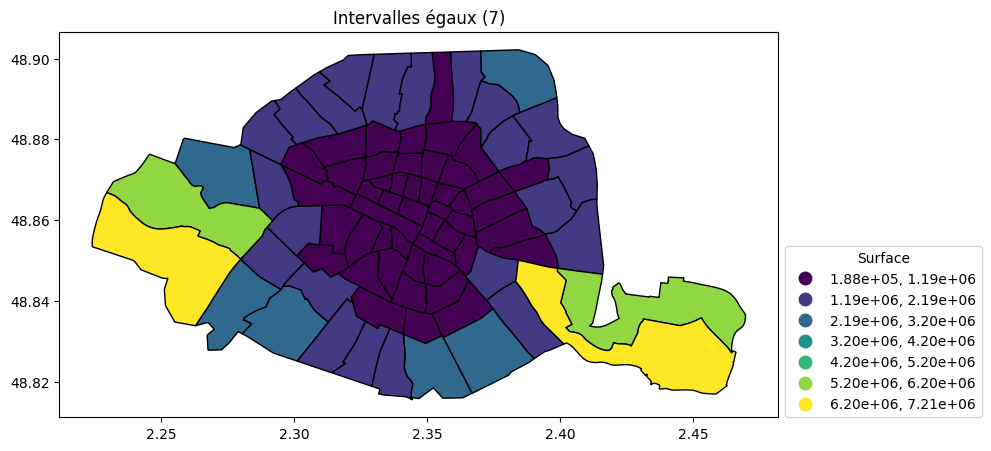

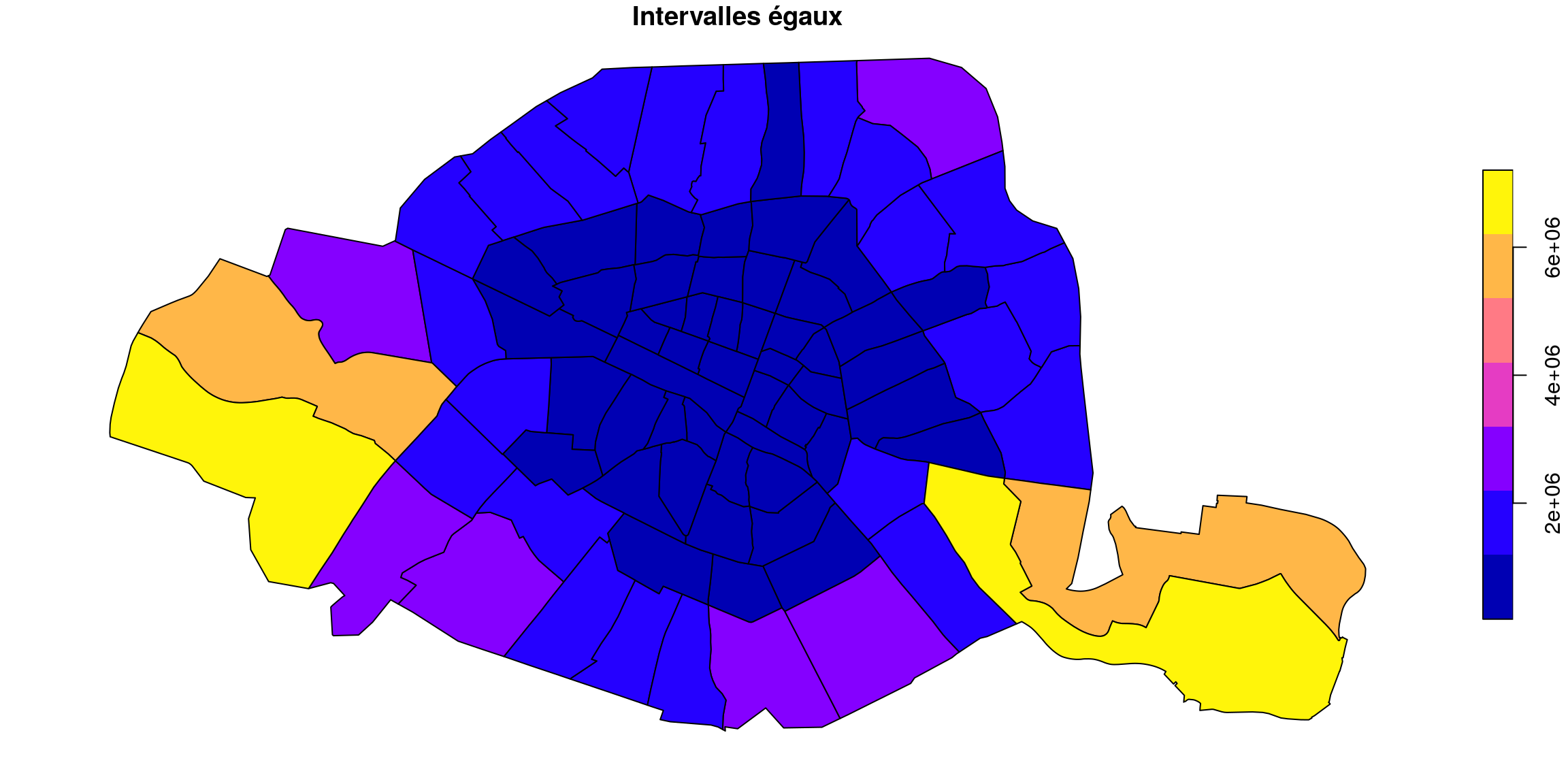
écart-types

quartier.plot(
	column="surface", scheme="stdmean", classification_kwds={"anchor":True}, legend=True, figsize=(15, 5),
	edgecolor="black", legend_kwds={"title": "Surface", "loc": (1.01, 0), "fmt": "{:.1e}"}
	).set_title("écart-types")

par(mar=c(0,0,0,0))
plot(quartiers["surface"], breaks="sd",main = "Écart-type")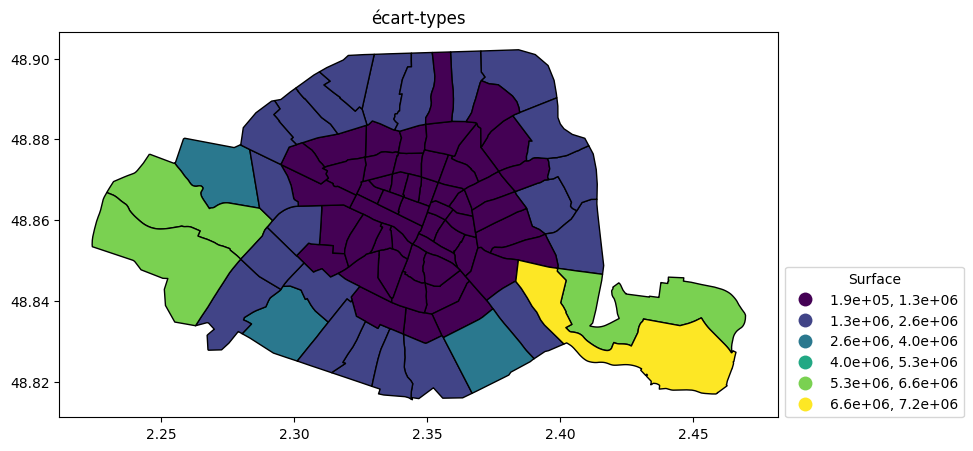

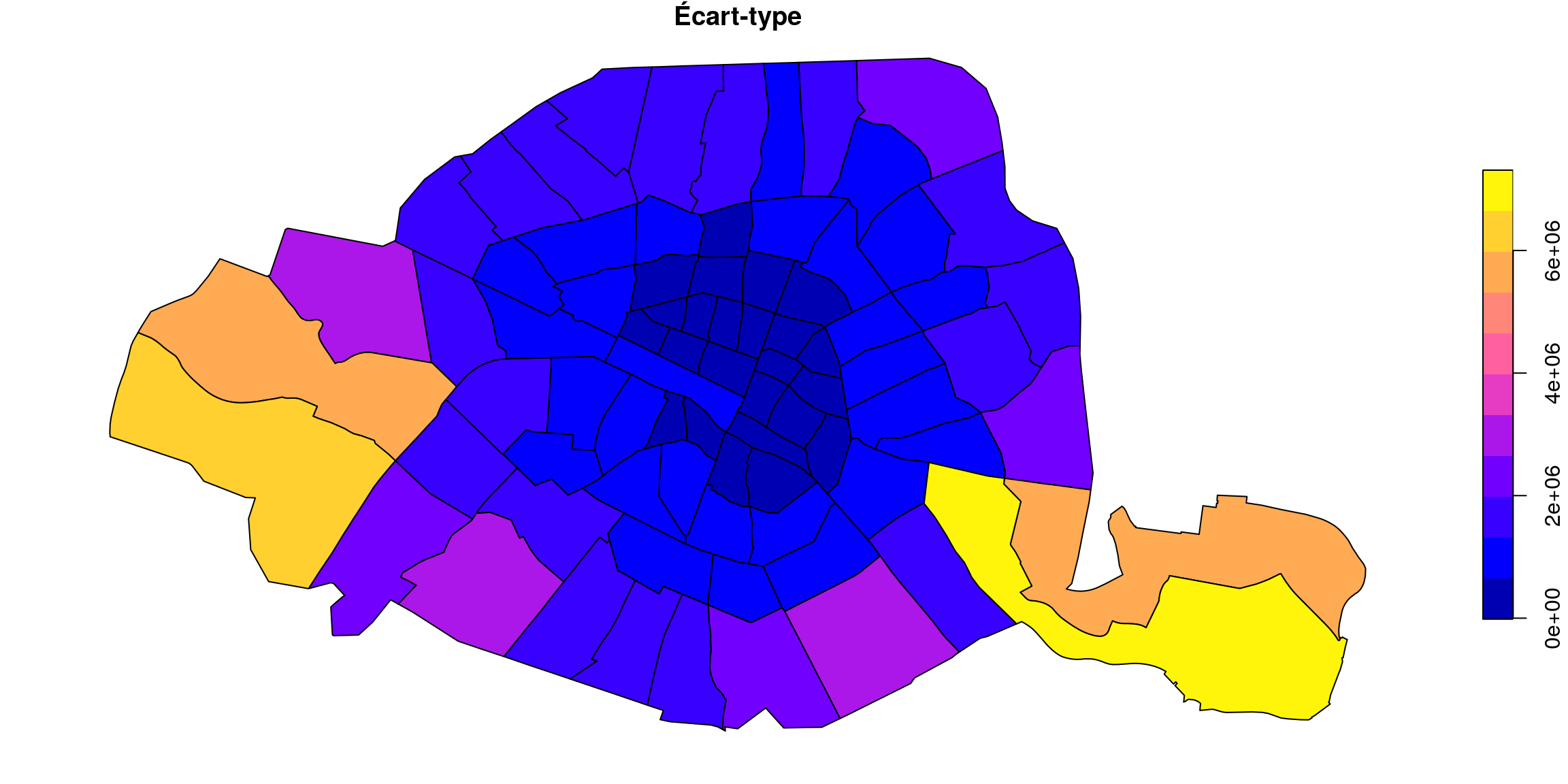
≈méthode des jolies ruptures sur variable centrée réduite

Guides de choix de la méthode de classification

Pour les classification manuelles :

Les classes doivent contenir toutes les valeurs, être sans recouvrement, contigües et distinctes.
Procéder par essai-erreur
Attention aux décimales et aux extrémités

Si distribution uniforme → Intervalles égaux
Si distribution asymétrique → Effectifs égaux, Jenks , progression géométrique (rare).
Si distribution symétrique → Écart-type, intervalle égaux

Autres classification

Consultez la documentation de la fonction classInt du package du même nom

Consultez la documentation du package mapclassify.

Transformations des données

⚠ D'abord effectuer une transformation linéaire pour ajuster le domaine de la variable afin que la transformation suivante soit définie et injective, = elle associe des valeurs distinctes à des résultats distincts

$x \mapsto log(x)$ pour une distribution asymétrique à droite ou
$x \mapsto \sqrt{x}$ si moins asymétrique.
$x \mapsto x^2$ pour une distribution asymétrique à gauche ou
$x \mapsto x^3$ si très asymétrique

(⚠ toujours vérifier l'allure de la distribution transformée)

Variables centrées-réduites

⚠ En principe, uniquement lorsque la distribution d’une variable est proche d’une gaussienne ⚠

Centrer : soustraire la moyenne.

Réduire : diviser par l'écart-type

Une variable centrée réduite est exprimée en «écarts-types à la moyenne»

→ permet de repérer les valeurs extrèmes (<-2σ ou >2σ)

→ utile pour comparer des individus selon un grand nombre de variables (tableaux de synthèse)

Visualiser une distribution

Histogramme
Distribution
BoxPlot
Violin plot
Pyramides (histogrammes juxtaposés)
Polygones de fréquences
Distribution cumulée, Fonction de répartition, CDF
Dot strip plot

Histogramme

from palmerpenguins import load_penguins
penguins = load_penguins()
penguins["body_mass_g"].dropna().plot(
    kind="hist", bins=50, xlabel="body mass [g]", ylabel="count",
    figsize=(15, 5), title="Penguins body mass\nhistogram", edgecolor="darkgray", color="darkorchid"
	)

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
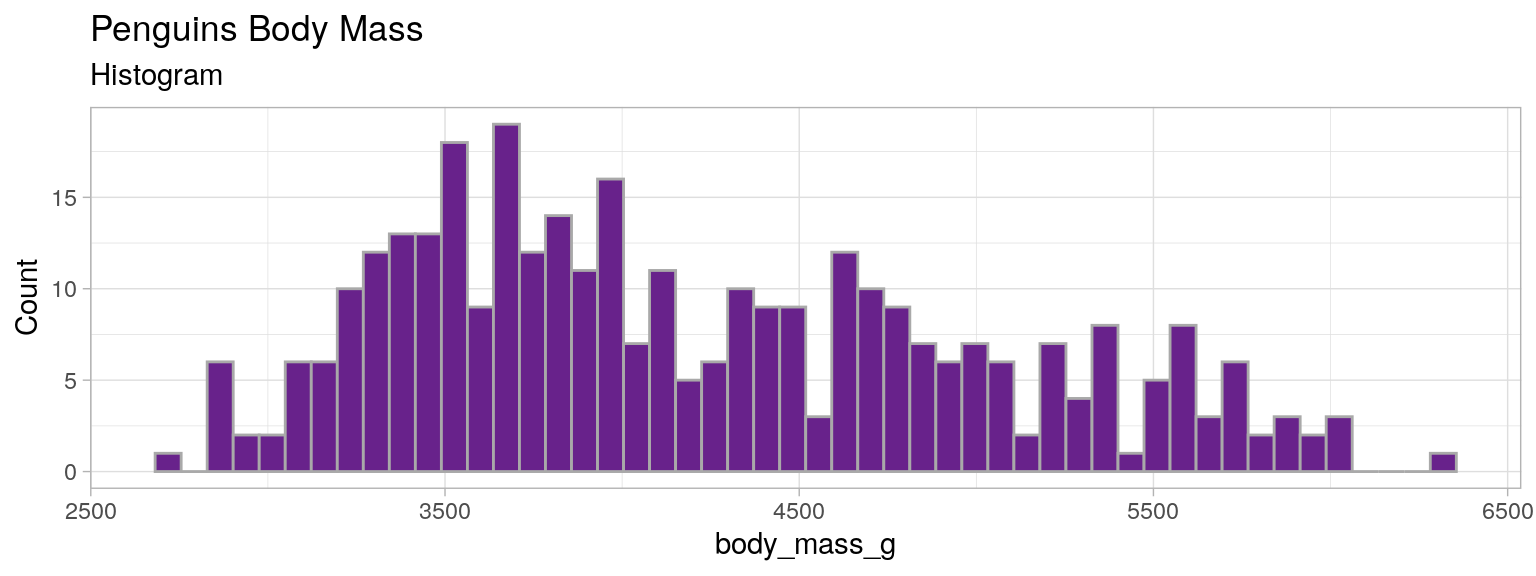
histo_mass <- ggplot(mydata)+
	geom_histogram(aes(x=body_mass_g), fill="darkorchid4", color="darkgray", bins=50)+
	labs(title = "Penguins Body Mass", subtitle = "Histogram")+
	ylab("Count")+theme_light()
histo_mass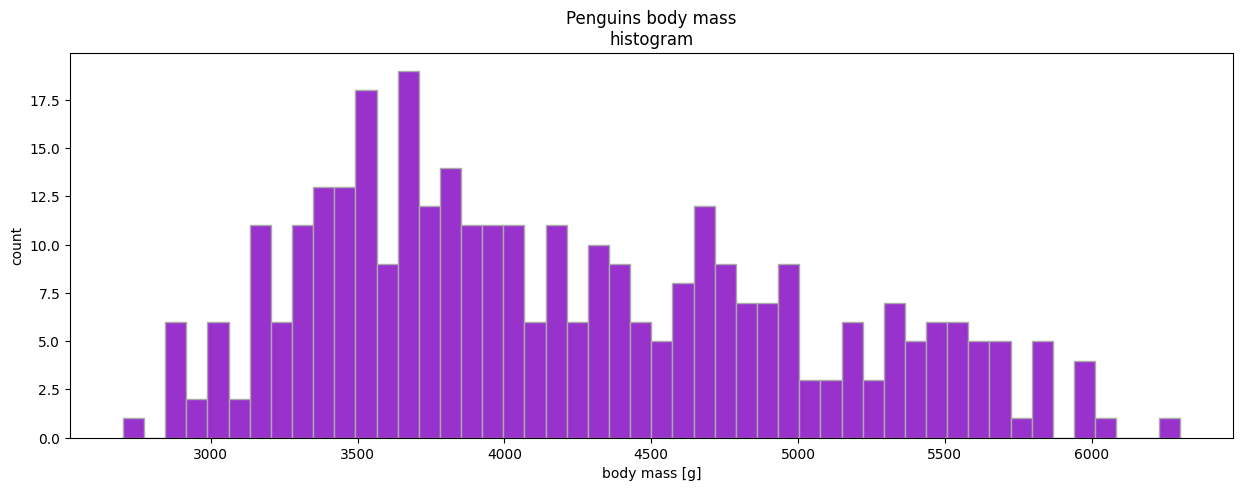

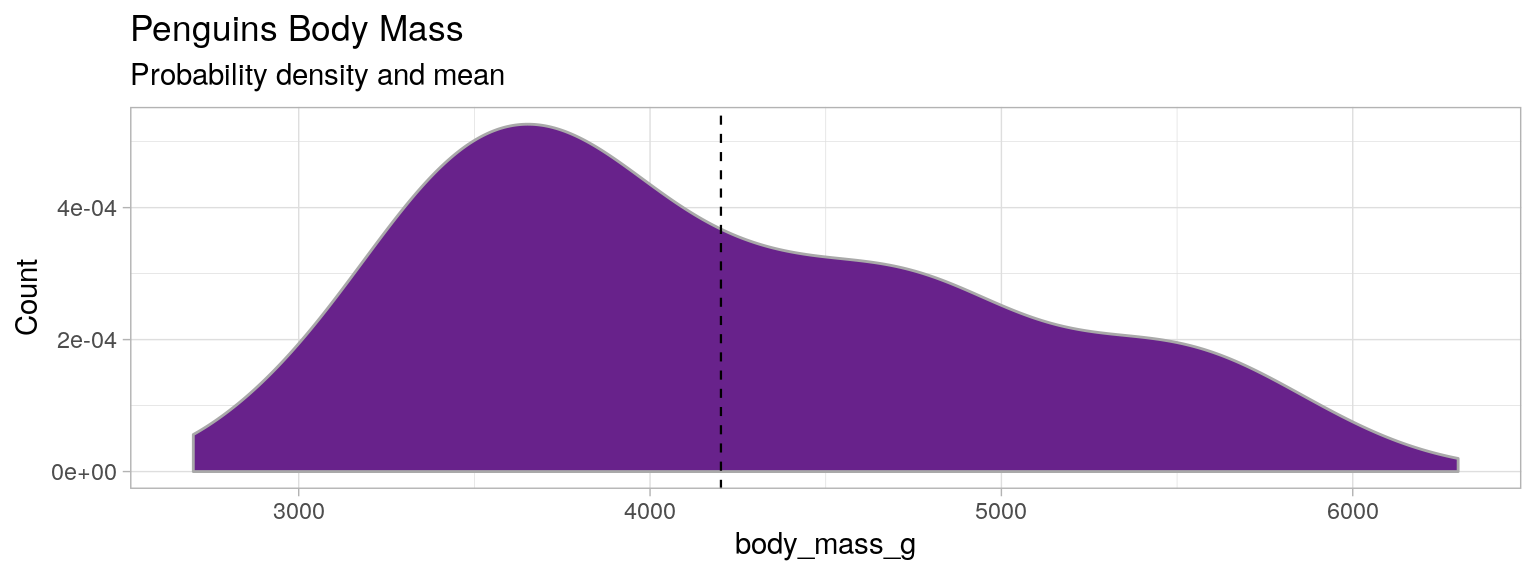
Distribution

⚠ ce n'est pas une probabilité, mais une densité de probabilité. Pour obtenir la probabilité, utiliser la formule $\mathbb{P}(a\leqslant X\leqslant b) = \int_a^b f(t)\,\mathrm{d}t$

ax = penguins["body_mass_g"].dropna().plot(
	kind="density",  ylabel="count",
	figsize=(15, 5), title="Penguins body mass\nProbability density and mean", color="darkorchid"
)
ax.axvline(x=penguins["body_mass_g"].dropna().mean(), color="black", linestyle="--")
ax.set_xlabel("body mass [g]")

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
distrib_mass <- ggplot(mydata)+
	geom_density(aes(x=body_mass_g), fill="darkorchid4", color="darkgray")+
	geom_vline(aes(xintercept=mean(body_mass_g, na.rm = T)), color="black", size=0.4, linetype="dashed" )+
	labs(title = "Penguins Body Mass", subtitle = "Probability density and mean")+
	ylab("Count")+theme_light()
distrib_mass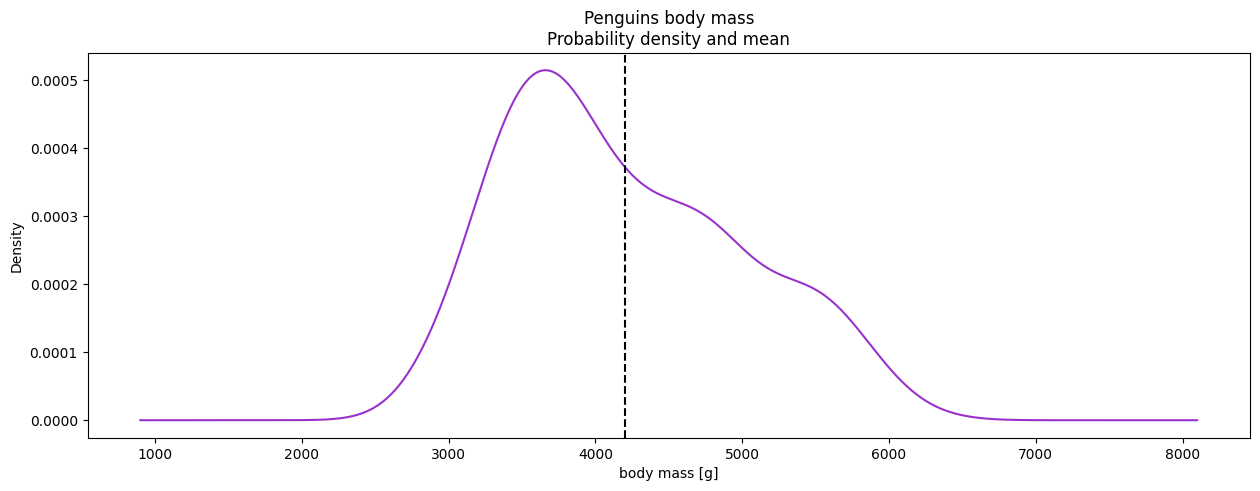

Boxplot

penguins.boxplot(
	column="body_mass_g", by="species", vert=False, figsize=(15, 5)
	).set_xlabel("body mass [g]")

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
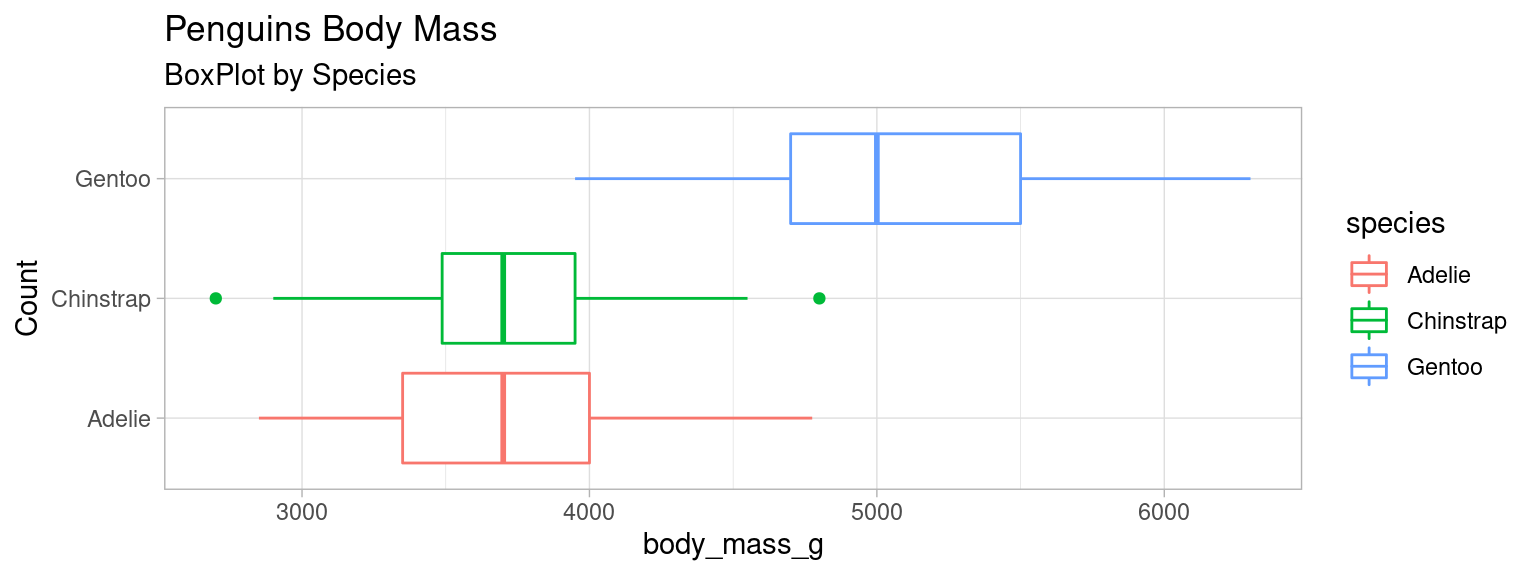
boxplot_mass <- ggplot(mydata)+
	geom_boxplot(aes(x=body_mass_g, y=species, color=species))+
	labs(title = "Penguins Body Mass", subtitle = "BoxPlot by Species")+
	ylab("Count")+theme_light()
boxplot_mass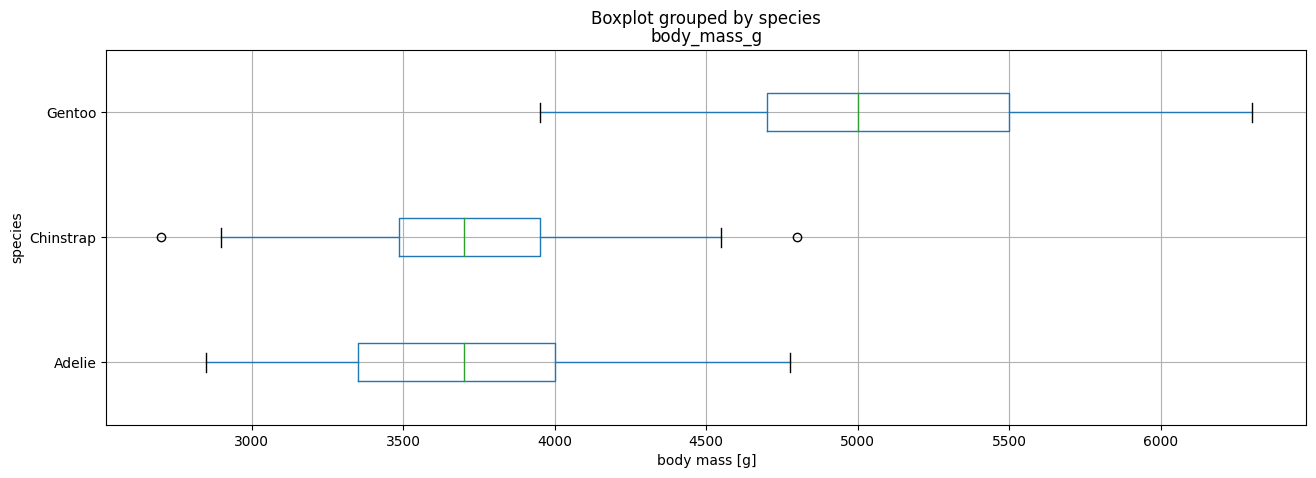

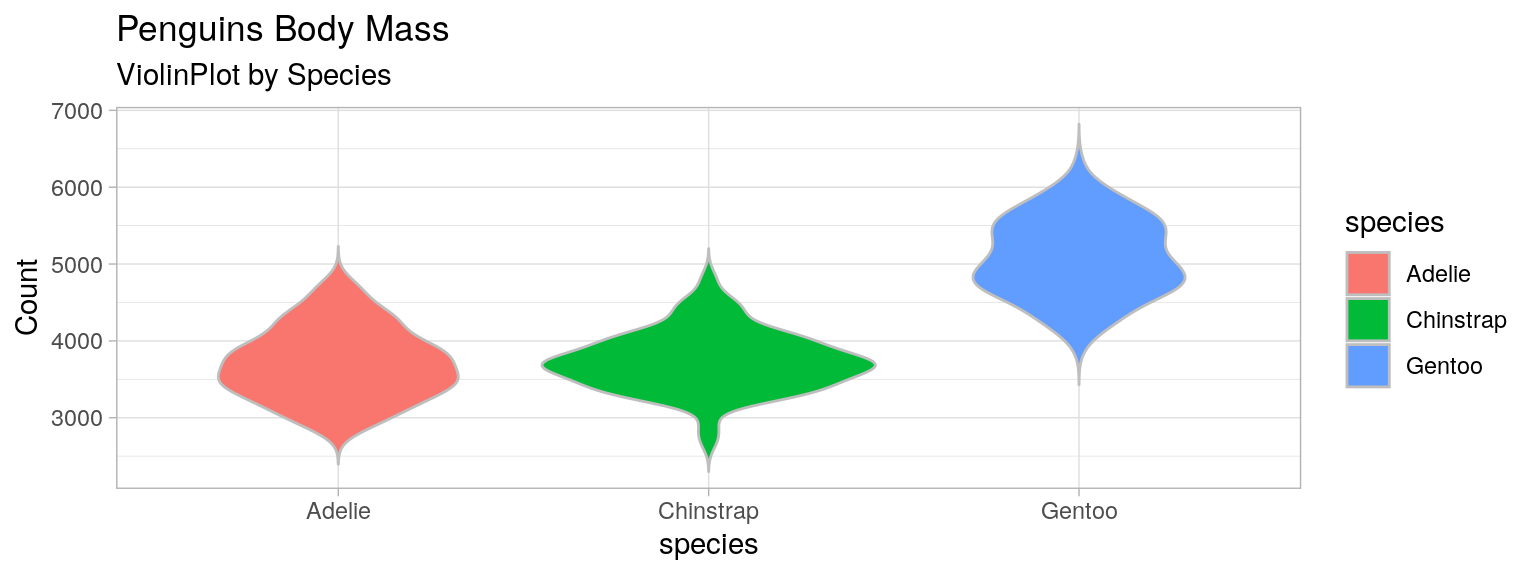
Violin Plot

Distribution + miroir. Utile pour des distributions complexes, mal résumées par la moyenne et la dispersion.

list_species = penguins["species"].unique()
plt.figure(figsize=(15, 5))
plt.violinplot(
	[penguins[penguins["species"]==species]["body_mass_g"].dropna() for species in list_species],   
)
plt.xticks(range(1, len(list_species)+1), list_species)
plt.xlabel("species", fontweight='bold')
plt.ylabel("body mass [g]")
plt.title("Penguins body mass\nviolin plot")

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
violin_mass <- ggplot(mydata)+
	geom_violin(aes(y=body_mass_g, x=species, fill=species), color="gray", trim=F)+
	labs(title = "Penguins Body Mass", subtitle = "ViolinPlot by Species")+
	ylab("Count")+theme_light()
violin_mass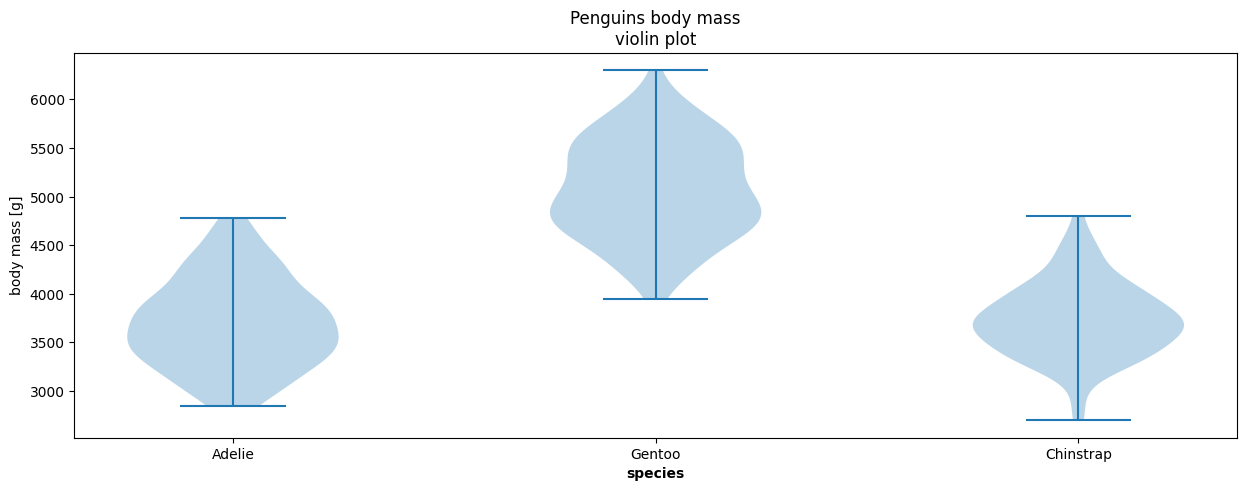

Violin Plot et boxplot

list_species = penguins["species"].unique()
plt.figure(figsize=(15, 5))
mass_groupby_species = [
	penguins[penguins["species"]==species]["body_mass_g"].dropna() for species in list_species
]
plt.violinplot(mass_groupby_species, showextrema=False)
plt.boxplot(mass_groupby_species, widths=0.1)
plt.xticks(range(1, len(list_species)+1), list_species)
plt.xlabel("species", fontweight='bold')
plt.ylabel("body mass [g]")
plt.title("Penguins body mass\nviolin plot and boxplot")

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
violin_mass <- ggplot(mydata)+
	geom_violin(aes(y=body_mass_g, x=species, fill=species), color="lightgray", trim=F)+
	geom_boxplot(aes(y=body_mass_g, x=species, fill=species), color="black", fill="#eeeeee" ,width=0.1)+
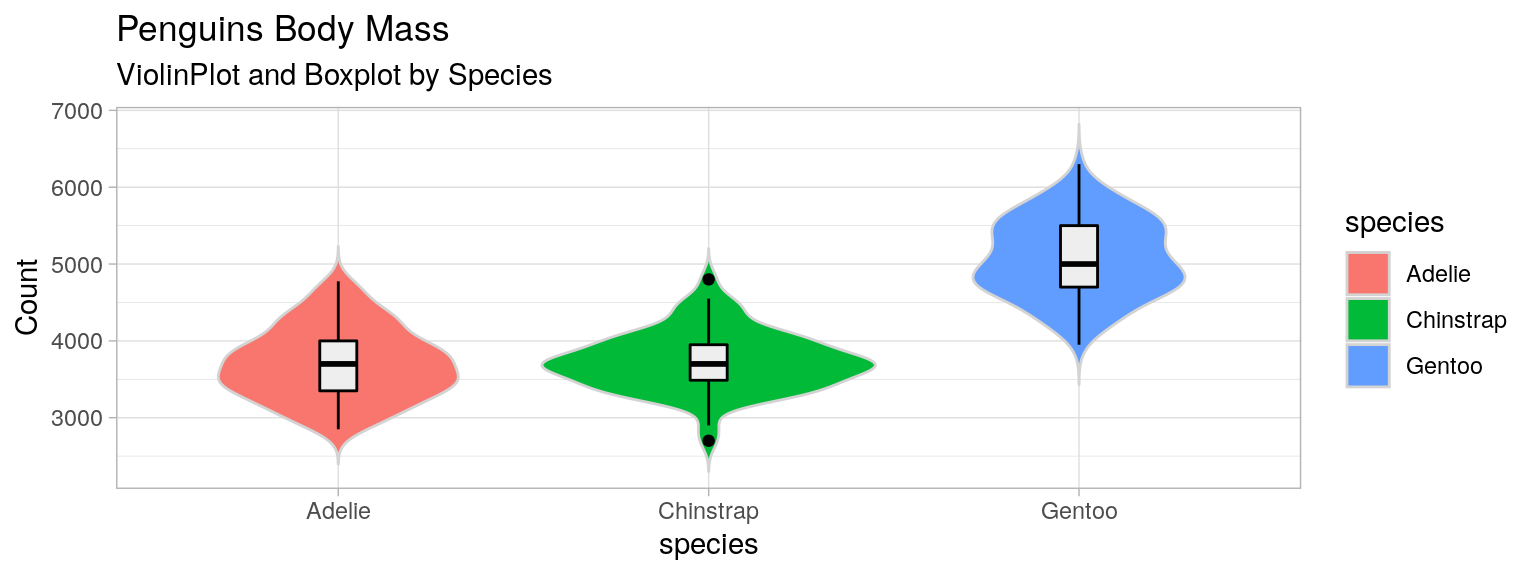
	labs(title = "Penguins Body Mass", subtitle = "ViolinPlot and Boxplot by Species")+
	ylab("Count")+theme_light()
violin_masss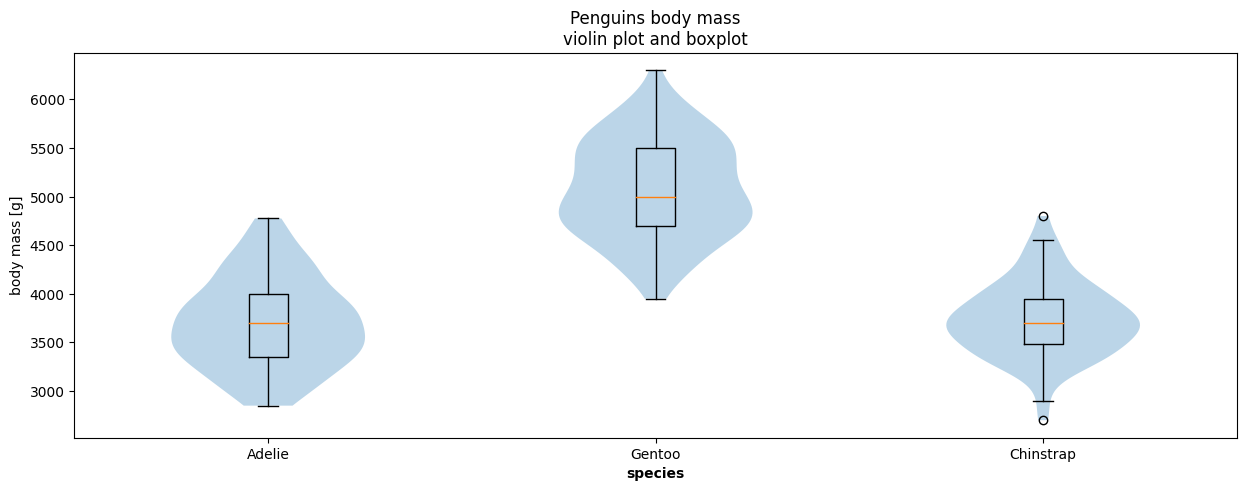

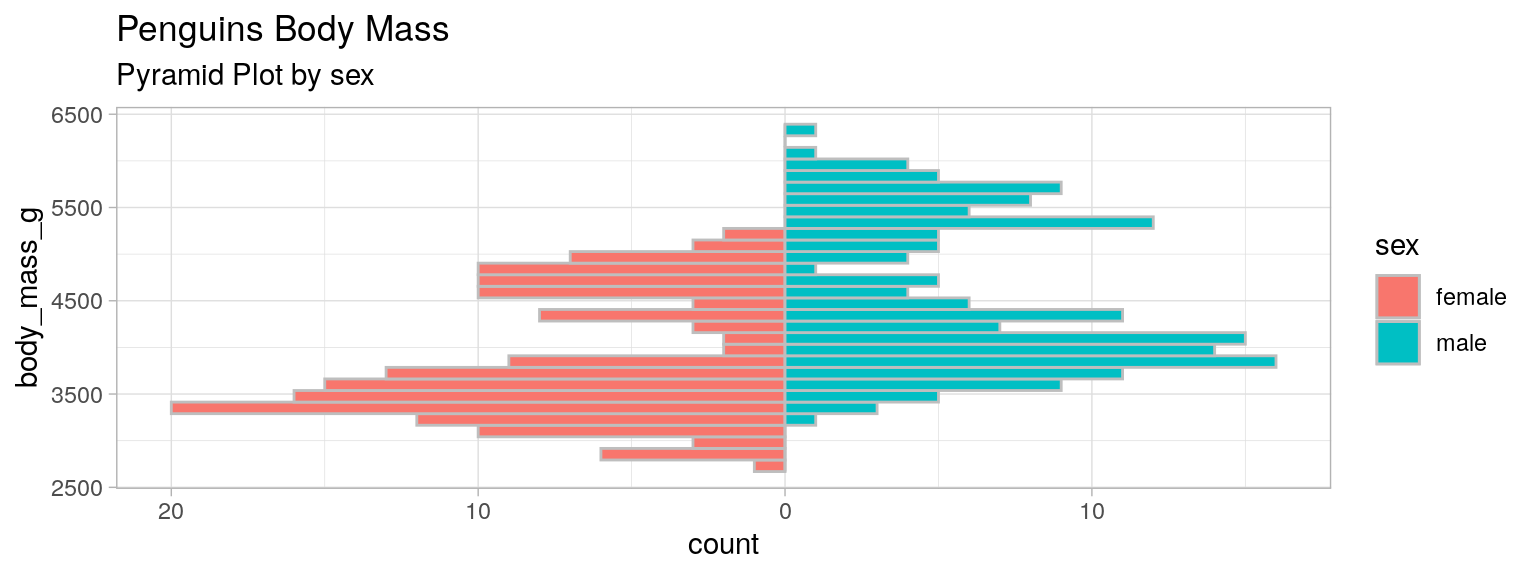
Pyramides (histogrammes juxtaposés)

Lorsqu'une des variables est qualitative à deux modalités :

female_data = penguins[penguins['sex'] == 'female']
male_data = penguins[penguins['sex'] == 'male']
female_count = np.histogram(female_data['body_mass_g'], bins=bins)[0]
male_count = np.histogram(male_data['body_mass_g'], bins=bins)[0]
bins = np.linspace(min(penguins['body_mass_g']), max(penguins['body_mass_g']), 50)
plt.barh(bins[:-1], male_count, height=np.diff(bins)[0], label='Male', edgecolor="grey")
plt.barh(bins[:-1], -female_count, height=np.diff(bins)[0], label='Female', edgecolor="grey")
ticks = np.arange(-max(female_count), max(male_count), 2)
plt.xticks(ticks=ticks, labels=np.abs(ticks))
plt.axvline(x=0, color='black'); plt.xlabel('Count'); plt.ylabel('Body Mass [g]')
plt.title('Penguins Body Mass\nPyramid Plot by Sex')
plt.legend()

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
pyramide_mass <-  ggplot(mydata, aes(fill = sex)) + 
	geom_bar(data = subset(mydata, sex == "female"), stat = "bin", aes(x=body_mass_g, y=..count..*(-1)), color="grey") +
	geom_bar(data = subset(mydata, sex == "male"), stat = "bin", aes(x=body_mass_g), color="grey") + 
	scale_y_continuous(labels = paste0(as.character(c(seq(20, 0, -10), seq(10, 20, 10))))) +
	ylab("count")+  coord_flip()+
	labs(title = "Penguins Body Mass", subtitle = "Pyramid Plot by sex")+
	theme_light()
	
pyramide_mass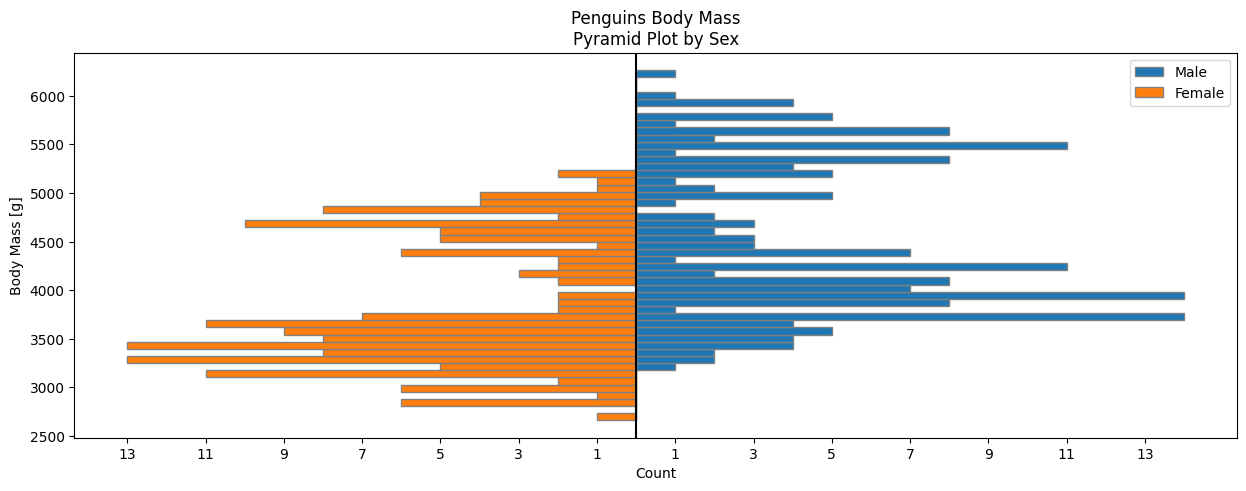

Polygones de fréquences

“Histogramme en courbe”
Utile pour comparer plusieurs distributions

bins = np.linspace(min(penguins['body_mass_g']), max(penguins['body_mass_g']), 50)
plt.figure(figsize=(15, 5))
for species in penguins["species"].unique():
	hist = np.histogram(penguins[penguins["species"] == species]["body_mass_g"], bins=bins)[0]
	plt.plot(bins[:-1]+np.diff(bins)/2, hist, label=species)
plt.legend(title="species")
plt.xlabel("body mass [g]")
plt.ylabel("count")
plt.grid(alpha=0.5)
plt.title("Penguins body mass\nFrequency polygons")

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
freqpoly_mass <- ggplot(mydata)+
	geom_freqpoly(aes(x=body_mass_g, color=species), bins=50)+
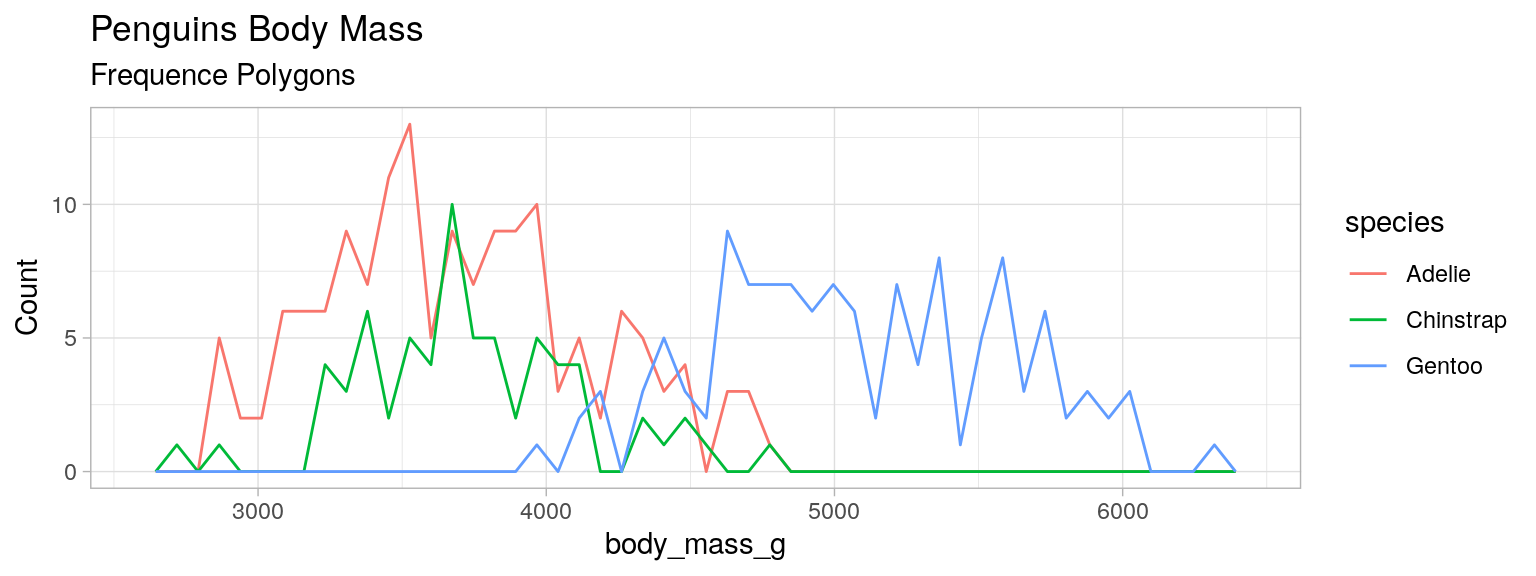
	labs(title = "Penguins Body Mass", subtitle = "Frequence Polygons")+
	ylab("Count")+theme_light()
freqpoly_mass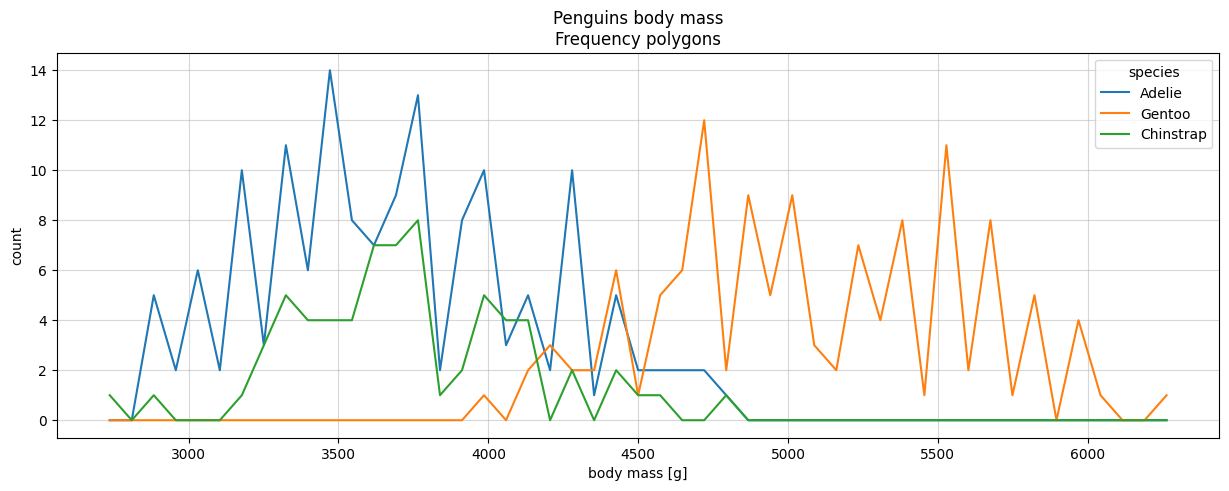

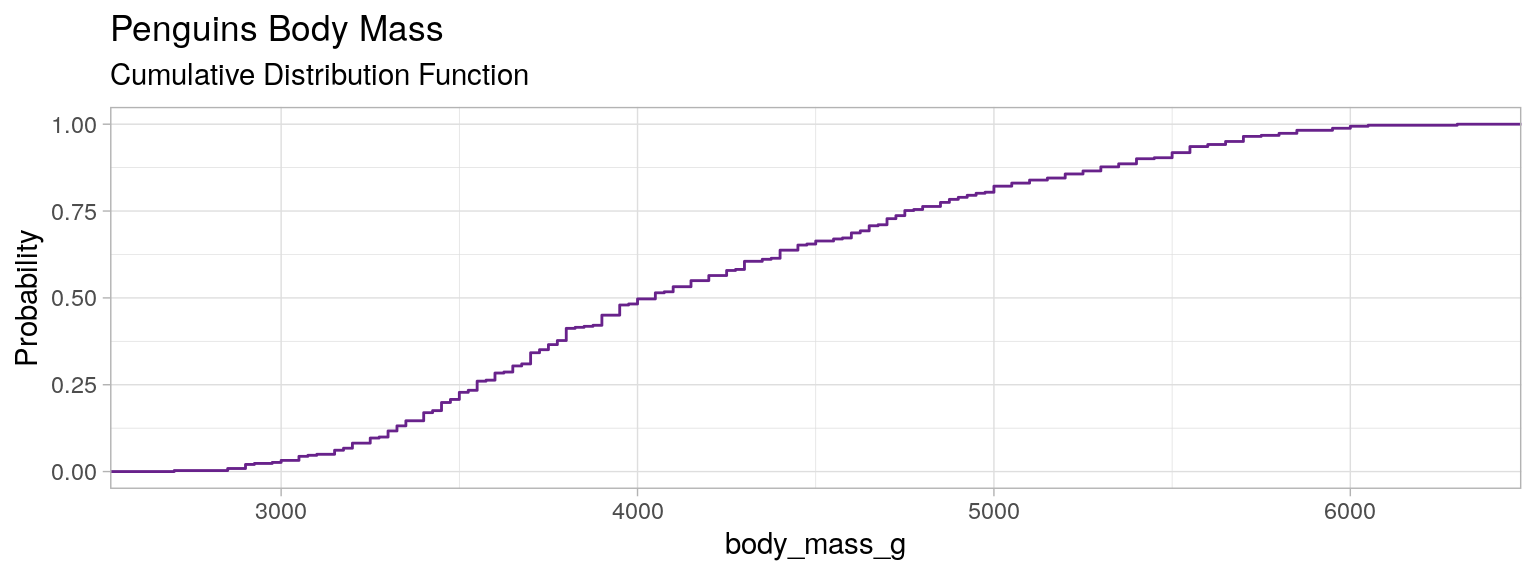
Distribution cumulée, Fonction de répartition, CDF

Courbe $x, y$,
en $x$ la valeur de la variable $V$, en $y$ la probabilité empirique d'avoir dans la population un individu pour lequel $V \leqslant x$

i.e. c'est la fonction :
$F_V(x) = \mathbb{P}(V\leqslant x)$

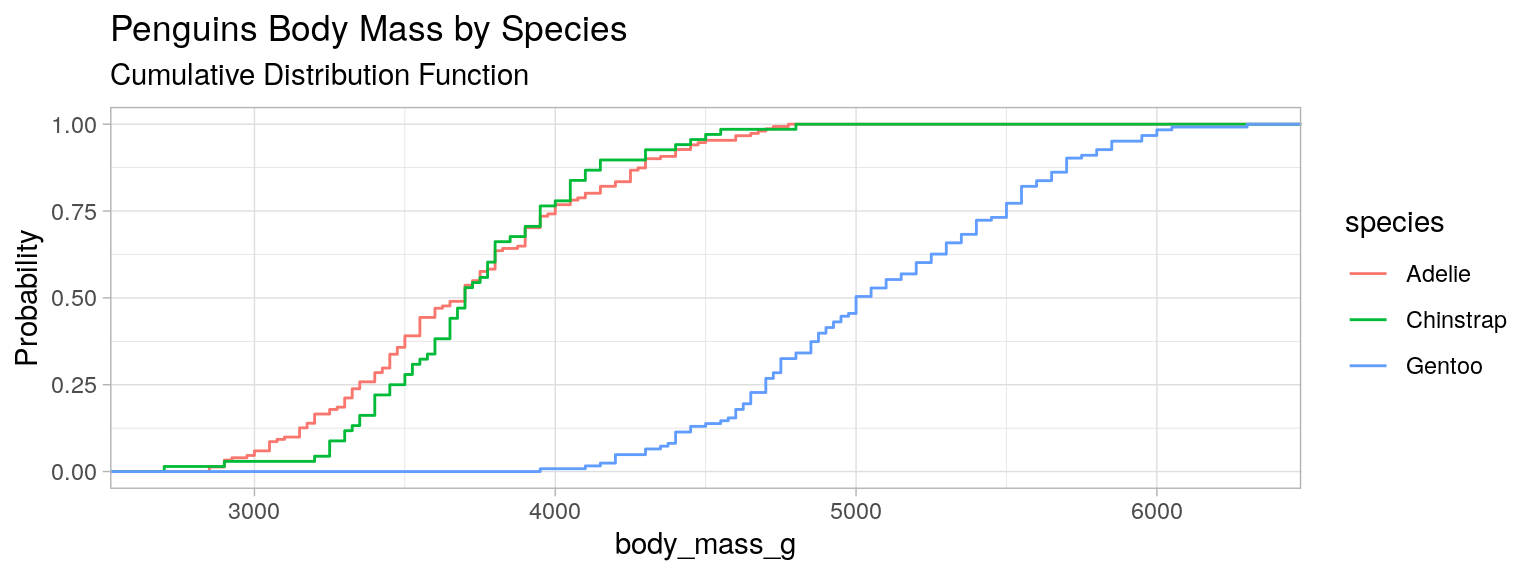
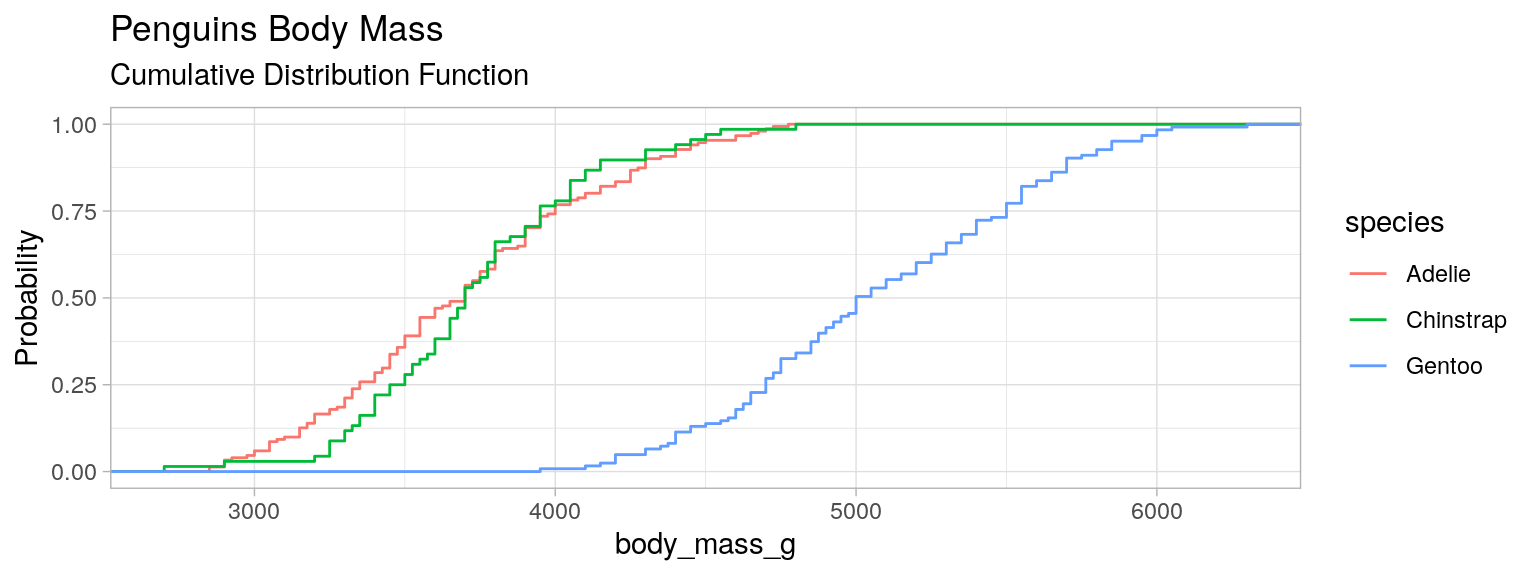
Distribution cumulée, Fonction de répartition, CDF

Permet de superposer les CDF de sous groupes de la population. Ici : les espèces des manchots.

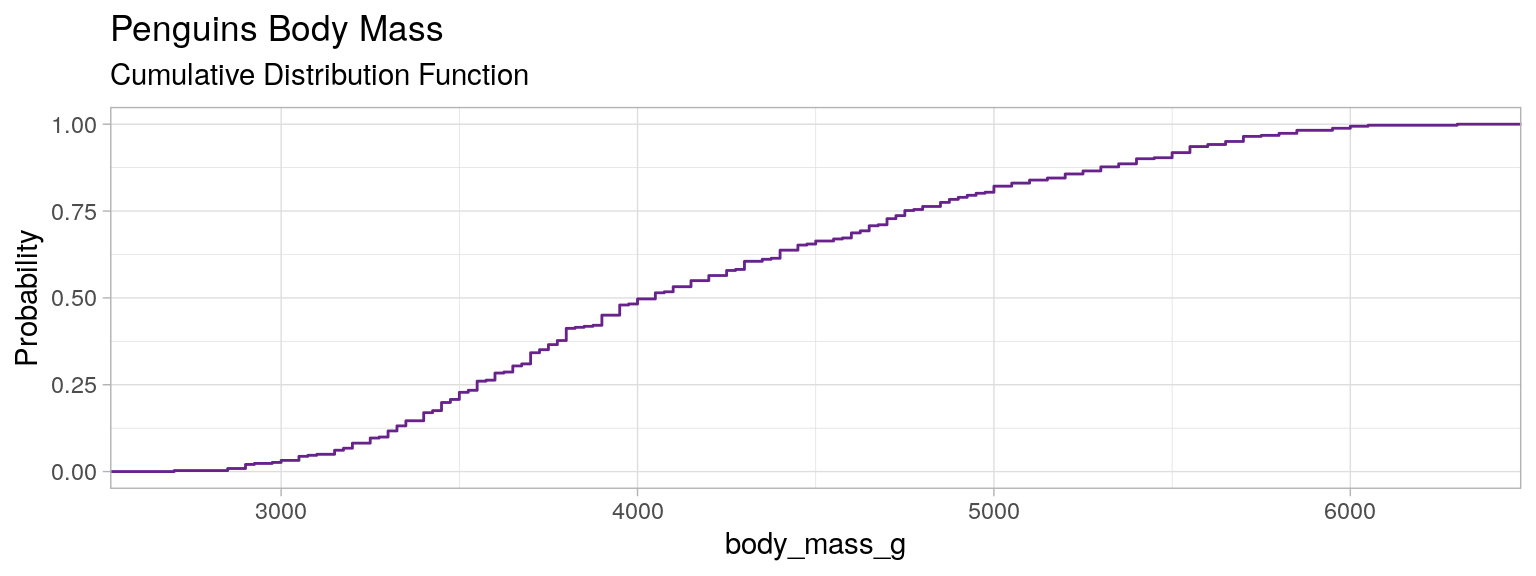
Distribution cumulée simple

plt.figure(figsize=(15, 5))
ax=plt.subplot()
plt.xlim((penguins["body_mass_g"].min(), penguins["body_mass_g"].max()))
penguins.plot(kind="hist", ax=ax, column="body_mass_g", density=True, histtype="step", cumulative=True, bins=len(penguins),
				title="Penguins Body Mass\nCumulative Distribution Function", ylabel="Probability", legend=False)
ax.set_xlabel("body mass [g]")
plt.grid(alpha=0.5)

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
plot_mass <- ggplot(mydata)+
	stat_ecdf(aes(x= body_mass_g),color="darkorchid4")+
	labs(title = "Penguins Body Mass", subtitle = "Cumulative Distribution Function")+
	ylab("Probability")+theme_light()
plot_mass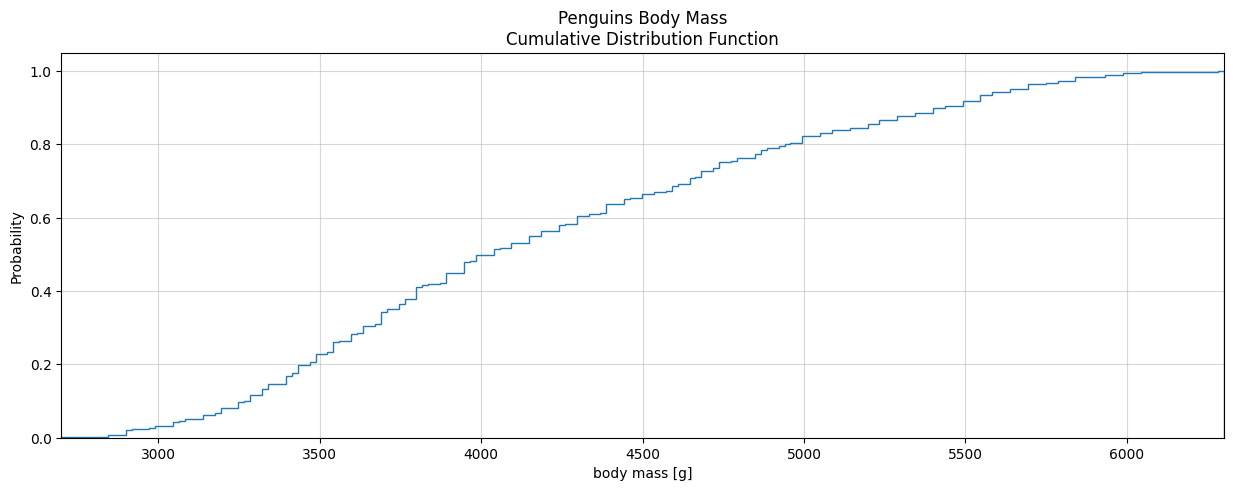

Distribution cumulée par groupe

plt.figure(figsize=(15, 5))
for species in penguins["species"].unique():
	plt.ecdf(penguins[penguins["species"] == species]["body_mass_g"], label=species)
plt.legend(title="species")
plt.xlabel("body mass [g]")
plt.ylabel("count")
plt.title("Penguins Body Mass\nCumulative Distribution Function")
plt.grid(alpha=0.5)

def ecdf(x, vmin, vmax,**kwargs):
	x = np.asarray(x)
	argsort = np.argsort(x)
	x = x[argsort]
	cum_weights = (1 + np.arange(len(x))) / len(x)
	line, = plt.plot([vmin, x[0], *x, vmax], [0, 0, *cum_weights, 1],
											drawstyle="steps-post", **kwargs)
	return line
plt.figure(figsize=(15, 5))
vmin = penguins["body_mass_g"].min()
vmax = penguins["body_mass_g"].max()
for species in penguins["species"].unique():
	ecdf(penguins[penguins["species"] == species]["body_mass_g"], vmin=vmin, vmax=vmax, label=species)
plt.legend(title="species")
plt.xlabel("body mass [g]")
plt.ylabel("count")
plt.title("Penguins Body Mass\nCumulative Distribution Function")
plt.grid(alpha=0.5)

library(palmerpenguins)
data(package = 'palmerpenguins')
mydata <-  penguins
plot_mass <- ggplot(mydata)+
	stat_ecdf(aes(x= body_mass_g,color=species))+    #on affecte la couleur à la variable modale  
	labs(title = "Penguins Body Mass", subtitle = "Cumulative Distribution Function")+
	ylab("Probability")+theme_light()
plot_mass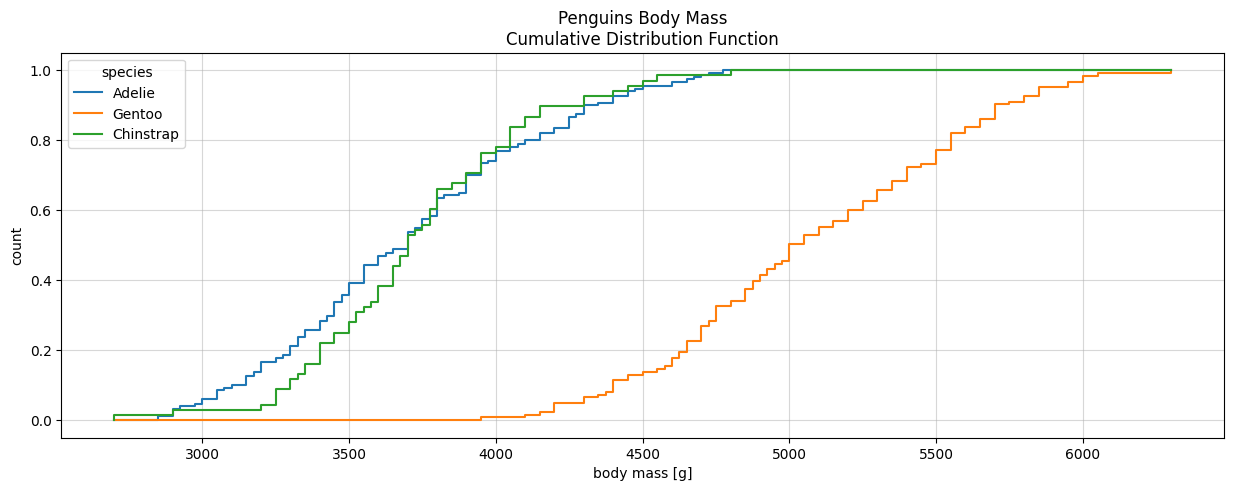

Bonus

Fat-tail distributions

Les distributions très asymétriques et très étendues sont délicates à résumer.

Les indicateurs traditionnels sont plus efficaces lorsque la variabilité des valeurs est moindre, et leur distribution plus symétrique.

e.g. Considérer la population moyenne des villes de France a-t’elle du sens ?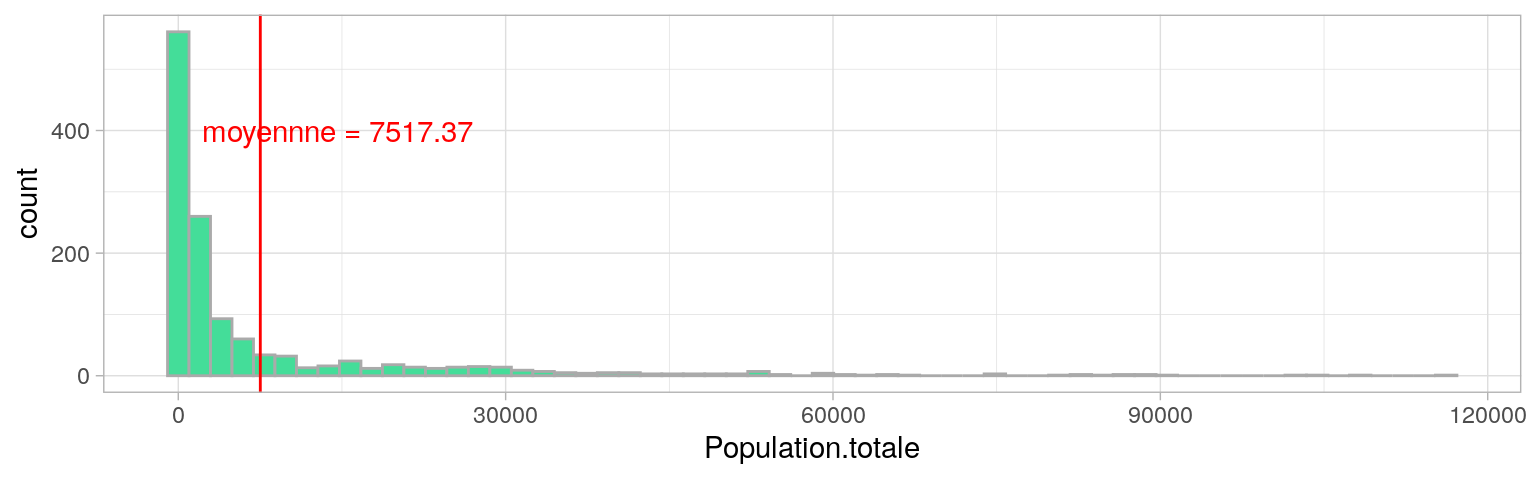

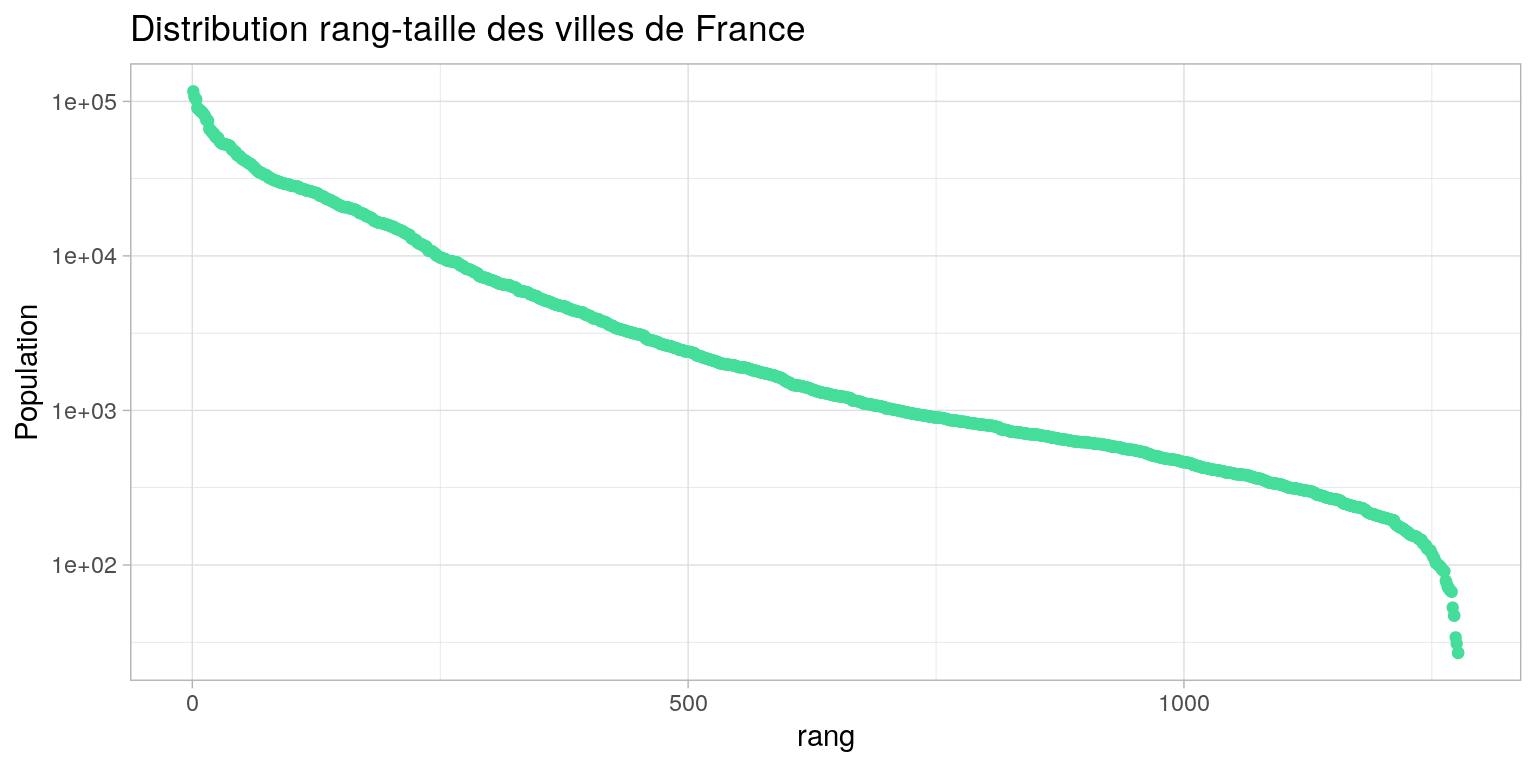
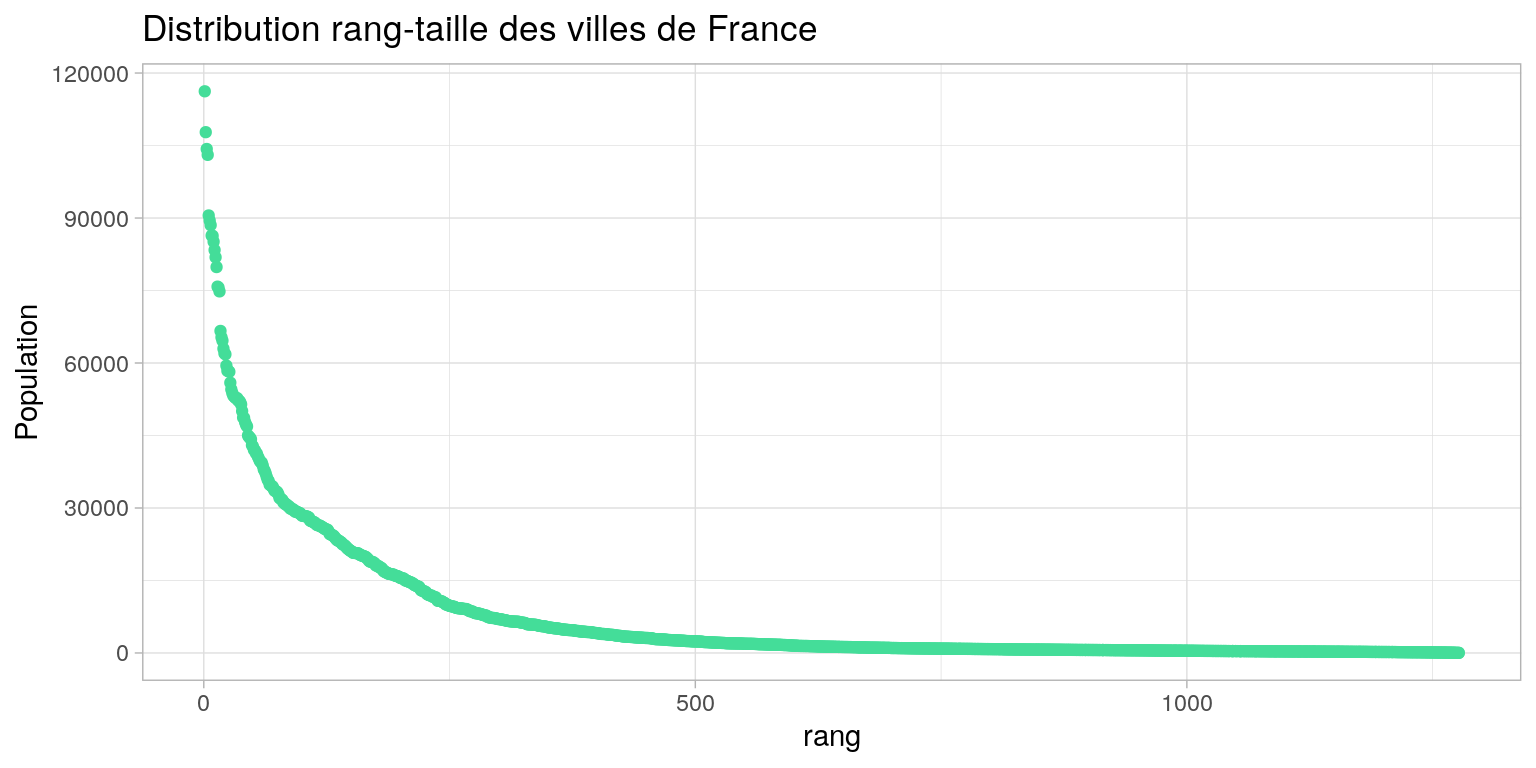
Distribution rang-taille des villes de france

Pour mieux voir la distribution et les écarts, on trace la taille des villes en fonction de leur rang

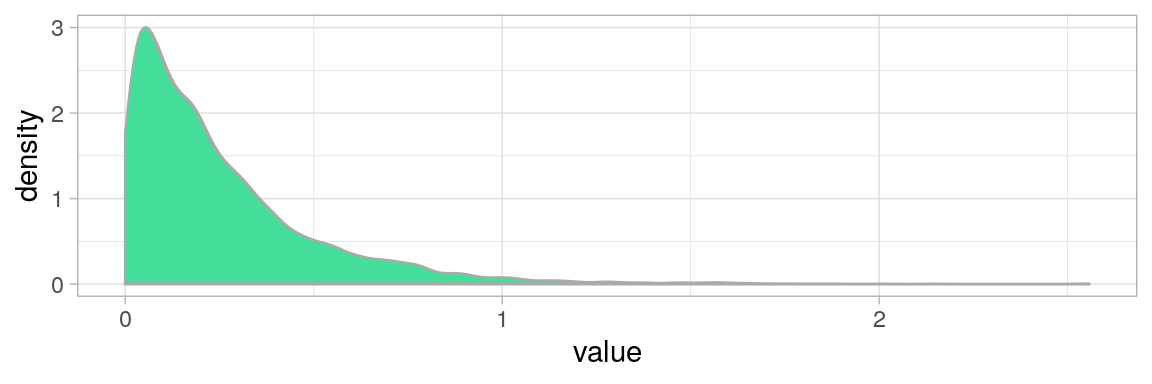
Transformation logarithmique

Appliquer une transformation monotone, bijective et inversible qui “applatisse” la distribution.

réduit les écarts entre les valeurs
resserre l’essentiel des valeurs

$\implies$ mesure de façon plus robuste tendance, dispersion et forme

Ici : le logarithme décimal