Chapitre 7 Autocorrélation spatiale : Moran et Geary
7.1 L’autocorrélation spatiale
La concentration d’un semis est mesurée par l’indice de concentration, qui décrit la régularité des positions des points.
Pour l’obtenir :
- on discrétise l’espace en \(C\) mailles de formes régulière( carrée, hexagonale)
- on calcule le nombre de points théorique par maille (la densité théorique) : \(D_{théo}= N/C\)
- on compte le nombre de points du semis par maille (la densité observée) et on calcule la variance de cette série : \[var(D_{obs}) = \frac{1}{C}\sum_c(nb_c-D_{théo})^2\]
avec:
- \(nb_c\), le nombre de points comptés dans la maille \(c\)
- \(C\) le nombre de maille du maillage
- \(N\) le nombre de points du semis.
L’indice de concentration est le ratio entre la densité et la variance du nombre de points par maille : \[IC= var(D_{obs})/D_{théo}\]
- si IC = 1 , la distribution est aléatoire
- si IC > 1 , la distribution est concentrée
- si IC < 1 , la distribution est homogène
Vous avez reconnu la comparaison -ici par un ratio- entre la distribution observée d’une quantité -la densité- et sa distribution théorique. De cette comparaison, on peut quantifier l’écart au modèle nul, ici une répartition aléatoire des objets.
comme dans le test du \(\chi^2\) , abordé en section 5.7.
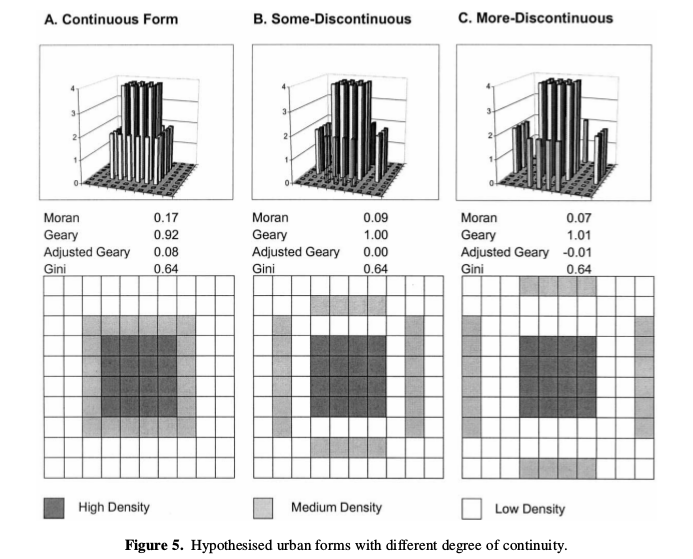
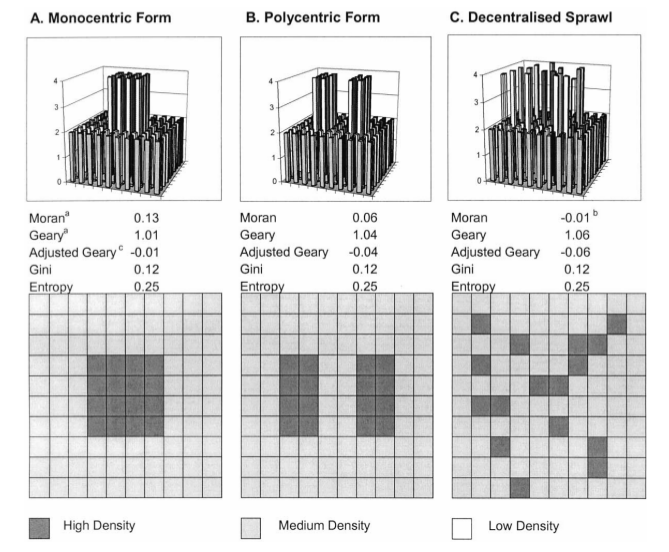
Voici quelques exemples de semis avec leur indice de concentration associés:
7.2 Auto-corrélation spatiale : Moran et Geary
L’auto-corrélation spatiale est une mesure statistique qui répond à la question suivante:
« Les valeurs d’entités spatiales proches sont-elles plus similaires que les valeurs d’entités lointaines ?»
«Est-ce que les grosses(resp. petites) valeurs sont rapprochées (resp.dispersées) ? »
E.g. (au hasard) Les personnes pauvres et les personnes riches sont-elles regroupées au même endroit dans une ville ?
Valeurs positives : situations ségrégées
Valeurs nulles : répartition aléatoire
Valeurs négatives : alternance parfaite entre valeurs
7.2.1 L’indice de Moran
L’indice \(I\) de Moran utilise un terme \(\omega_{ij}\) positif d’“interaction” pour quantifier la proximité entre deux entités \(i\) et \(j\).
On peut le choisir discret (1 si voisins , 0 sinon) ou continu (inverse de la distance).
\(I=\frac{n}{\sum_i \sum_j \omega_{ij}} \frac{\sum_i \sum_j \omega_{ij}(X_i-\bar{X})(X_j-\bar{X})}{\sum_i(X_i-\bar{X})^2}\)
avec \(n\) le nombre d’entités spatiales ,
\(\omega\) une matrice carrée de poids positifs de dimension \(n\), telle que \(\omega_{ij}\) quantifie la proximité, l’influence de \(j\) sur \(i\) ,
\(\bar{X}\) la moyenne de la variable \(X\)
7.2.2 L’indice de Geary
Cet indice, noté \(C\), est dit plus “local” que l’indice de Moran
\(C=\frac{(n-1) \sum_i \sum_j \omega_{ij}(X_i-X_j)^2 }{2W\sum_i(X_i-\bar{X})^2}\)
\(C\in[0;2]\)
\(C<1\) : auto-corrélation négative,
\(C=1\) : pas d’autocorrelation,
\(C>1\) : autocorrélation positive
avec
\(n\) le nombre d’entités spatiales,
\(\omega\) une matrice carrée de poids positifs de dimension \(n\), de somme \(W\) et telle que \(\omega_{ij}\) quantifie la proximité, l’influence mutuelle de \(j\) sur \(i\), \(\bar{X}\) la moyenne de la variable \(X\)
7.3 Les flux
7.3.1 Matrice de flux
Pour une partition en zones d’un espace, on appelle flux toute mesure d’intéraction spatiale qui implique des échanges, des déplacements entre deux zones, matériels ou immatériels.
On range les mesures qui mesurent ces échanges dans un matrice de flux,une matrice carrée \(F\) dont le terme général \(F_{ij}\) indique la quantité échangée entre le site \(i\) en ligne et le site \(j\) en colonne .
7.3.2 Indices
\(V_i= \sum_i F_{ij} + \sum_j F_{ij}\) : Volume = Départs + Arrivées
\(S_i = \sum_i F_{ij} - \sum_j F_{ij}\) : Solde= Départs - Arrivées
\(A_i = \frac{S_i}{V_i}\) : Attractivité = ratio des soldes sur les volumes
7.3.3 Cartographie des flux
On en peut pas représenter tous les flux entre toutes les zones (lisibilité).
On détermine les flux dominants de la façon suivante:
\(F_{ij}\) est dominant si:
- \(i\) envoie son flux le plus important vers \(j\)
- la somme des arrivées de \(j\) est plus importante que la somme des arrivées de \(i\)
package flows de R : https://cran.r-project.org/web/packages/flows/vignettes/flows.html par les auteurs de cartography
7.4 Exemple
## Reading layer `urban_area' from data source `/home/paulchapron/R/x86_64-pc-linux-gnu-library/4.1/flows/gpkg/GE.gpkg' using driver `GPKG'
## Simple feature collection with 159 features and 2 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: 691189 ymin: 6562692 xmax: 1070595 ymax: 7009226
## Projected CRS: RGF93 v1 / Lambert-93## Reading layer `region' from data source `/home/paulchapron/R/x86_64-pc-linux-gnu-library/4.1/flows/gpkg/GE.gpkg' using driver `GPKG'
## Simple feature collection with 1 feature and 0 fields
## Geometry type: POLYGON
## Dimension: XY
## Bounding box: xmin: 688355 ymin: 6562692 xmax: 1082671 ymax: 7009226
## Projected CRS: RGF93 v1 / Lambert-93
## 95 'NA' values are not plotted on the map.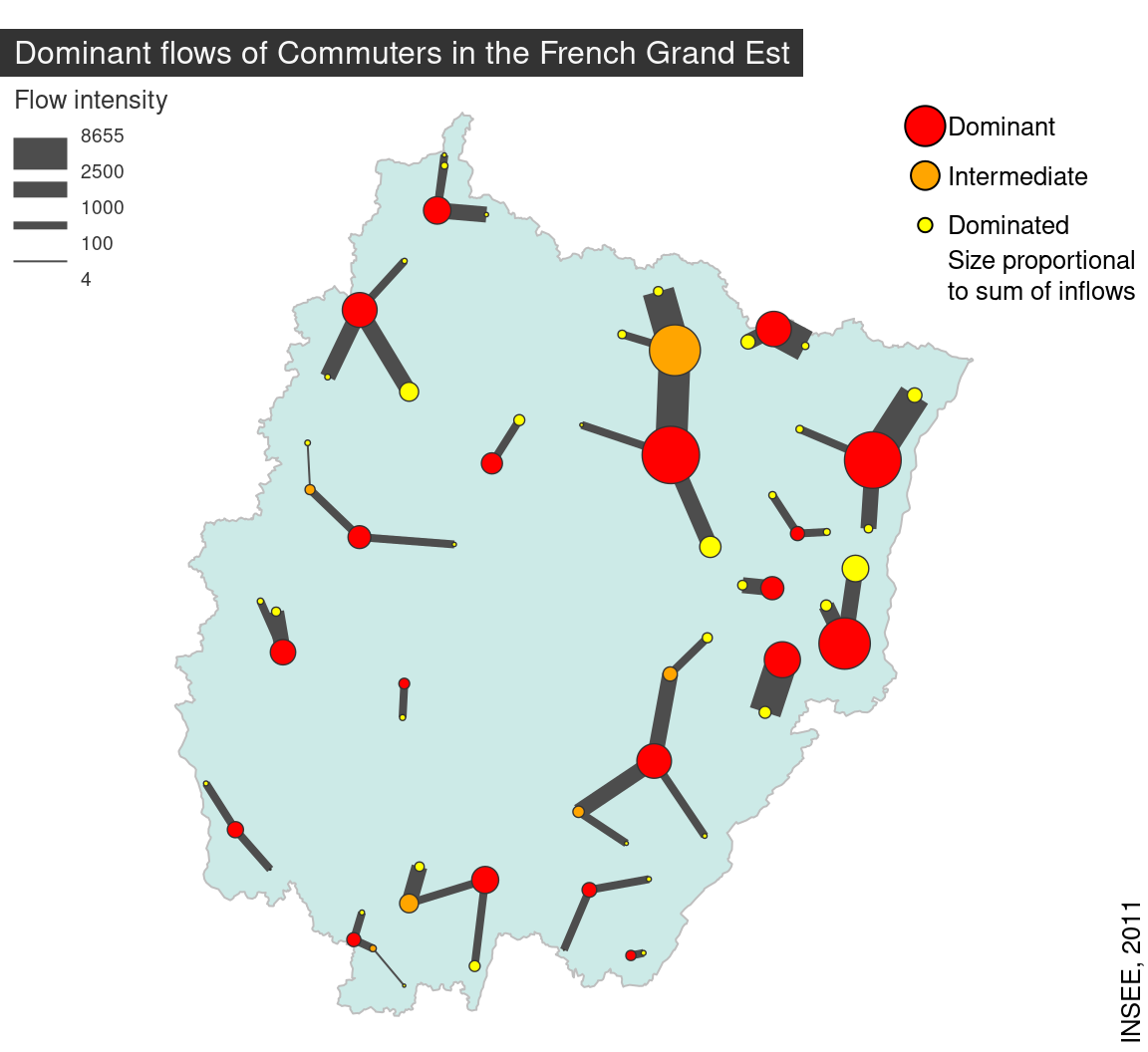
7.4.1 Pour aller plus loin
les flux sont modélisés par des graphes, une grande partie de la littérature de l’analyse de réseaux et des notions de théories des graphes peuvent être transposées et utilisées pour l’analyse de flux.
E.g. Attributs de noeuds ou d’arcs :
- centralité de degré (nombres de voisins dans le graphe)
- centralité d’intermédiarité (fréquence d’apparition du noeud dans les plus courts chemins entre deux noeuds du graphe)
Attributs de graphes :
- communautés (sous graphes denséments connectés)
- densité de liens
- …
7.5 Le modèle gravitaire
7.5.1 Fin XIXe : Les lois de Ravenstein
(Ravenstein E., 1885 & 1889, “The Laws of Migration”, Journal of Royal Statist. Society, London , d’après Noin D., 1988, Géographie de la Population, Masson, Paris, pp. 273-274, cité par C. Grasland.
Le nombre de migrants diminue quand la distance augmente; la plupart ne vont pas très loin ; ceux qui se déplacent sur de grandes distances se dirigent de préférence vers les grands centres commerciaux et industriels.
Le processus se fait de la façon suivante : une ville à croissance rapide attire les gens des régions environnantes ; les vides ainsi créés sont comblés par les migrants de districts plus éloignés ; la force d’attraction des grandes villes dynamiques se fait donc sentir de proche en proche en diminuant d’intensité. Le nombre de migrants de la zone d’accueil est donc proportionnel à la population de la zone d’origine et inversement proportionnel à la distance qui les sépare.
Chaque courant principal de migration suscite un contre-courant compensatoire.
Les citadins ont une mobilité plus faible que les ruraux
Les femmes ont une mobilité plus forte que les hommes, au moins à courte distance.
L’intensité des migrations augmente avec le développement du commerce, de l’industrie et des transports
Les facteurs déterminant la migration sont nombreux mais le plus important est le facteur économique
7.5.2 Le modèle gravitaire
Modèle simple, déterministe et symmétrique qui prose de calculer l’intensité de l’interaction entre deux entités spatiales en fonction de leurs masses et de la distance qui les sépare.
Plusieurs formulations :
\(Fij = k \frac{P_i . P_j}{D_{ij}^2}\)
avec \(P_i\) la masse (e.g. population, attraction, emmission, etc.) de l’entité spatiale \(i\), \(D_ij\) une fonction de coût e.g. la distance qui sépare \(i\) de \(j\)
\(Fij = k \frac{P_i . P_j}{D_{ij}^\alpha}\)
avec alpha le frein à la distance (distance decay) , pour modéliser des déplacements plus ou moins faciles
7.5.3 Distance et interaction
D’après H.Commenges, cours d’analyse spatiale , Delhi R School
Lorsque l’interaction est spatialisée, elle implique nécessairement une distance.
- L’interaction spatiale considère le déplacement comme un effort.
- L’interaction spatiale est le rapport dialogique entre mise en contact et friction de l’éloignement.
- L’interaction spatiale être abordée de deux façons : relations entre lieux ou attraction/influence d’un lieu sur les autres lieux.
- Dans le premier cas on parlera d’analyse de flux
- Dans le second cas on parlera d’analyse de position (cf. Accessibilité)
7.5.4 Utilisation du modèle gravitaire
Exemple d’une formulation plus générale : \(F_{ij} = \alpha_i \beta_j E_i A_j C_{ij}^{−n}\)
avec \(\alpha_i\) et\(\beta_j\) des facteurs d’équilibrage qui assurent la contrainte aux marges,
\(E_i\) et \(A_j\) : valeurs d’émission et d’attraction de la zone
\(C_{ij}\) : coût généralisé du trajet de \(i\) vers \(j\) : temps, prix , inconfort.
\(n\) : frein à la distance, la valeur varie selon les motifs de déplacement. (plus faible vers le travail que vers des motifs “secondaires” (e.g. courses quotidiennes)
On détermine les valeurs des coefficients (\(\alpha,\ \beta,\ n\))inconnus par calibration sur des données (problème d’optimisation classique, qu’on peut résoudre par algorithme génétique, recuit simulé, etc.)
7.6 L’étape d’après : modèles dynamiques
Les modèles que nous avons jusqu’à présent étaient des modèles statiques: ils décrivaient ou résumaient des données par des objets mathématiques eux aussi “statiques”.
Nous avons vu le modèle linéaire , qui résume une nuage de points lorsqu’il a la forme appropriée. Cet objet est fixe, il s’agit des deux coefficient d’une équation de droite \(y=ax+b\), et \(a\) et \(b\) une fois déterminés n’ont pas vocation à évoluer.
7.6.1 Modèles simples : les automates cellulaires
Le plus célèbre des modèles simples : le jeu de la vie (Conway)
Modèle de ségrégation de Schelling


7.6.2 Principe d’un modèle complexe de mobilité
Modèle à 4 étapes
Module de génération : quantité de déplacements attirés et émis par zones prédécoupées (caractéristiques de la population et des activités)
Module de distribution : répartition géographique des flux (modèle gravitaire)
Module de choix modal : par quel modalité s’effectue le transport ?
Module d’affectation au réseau
Modèles LUTI : Land Use Transport Integration
Accessibilité et Usage du sol exercent une influence l’un sur l’autre.
Simule les foyers, leurs choix de résidence , d’activité et de transports.