Chapitre 6 La Forme
La forme d’une distribution est décrite par deux caractéristiques : sa symétrie (ou son asymétrie) et son applatissement.
Chapitre 6 La Forme
La forme d’une distribution est décrite par deux caractéristiques : sa symétrie (ou son asymétrie) et son applatissement.
6.1 Asymétrie
L’asymétrie d’une distribution est positive si les valeurs fréquentes sont à gauche et la queue de distribution (due à quelques valeurs très élevées surreprésentées) est à droite .
L’asymétrie est négative si les valeurs fréquentes sont à droite et la queue de distribution (due à des valeurs très faibles surreprésentées) est à gauche
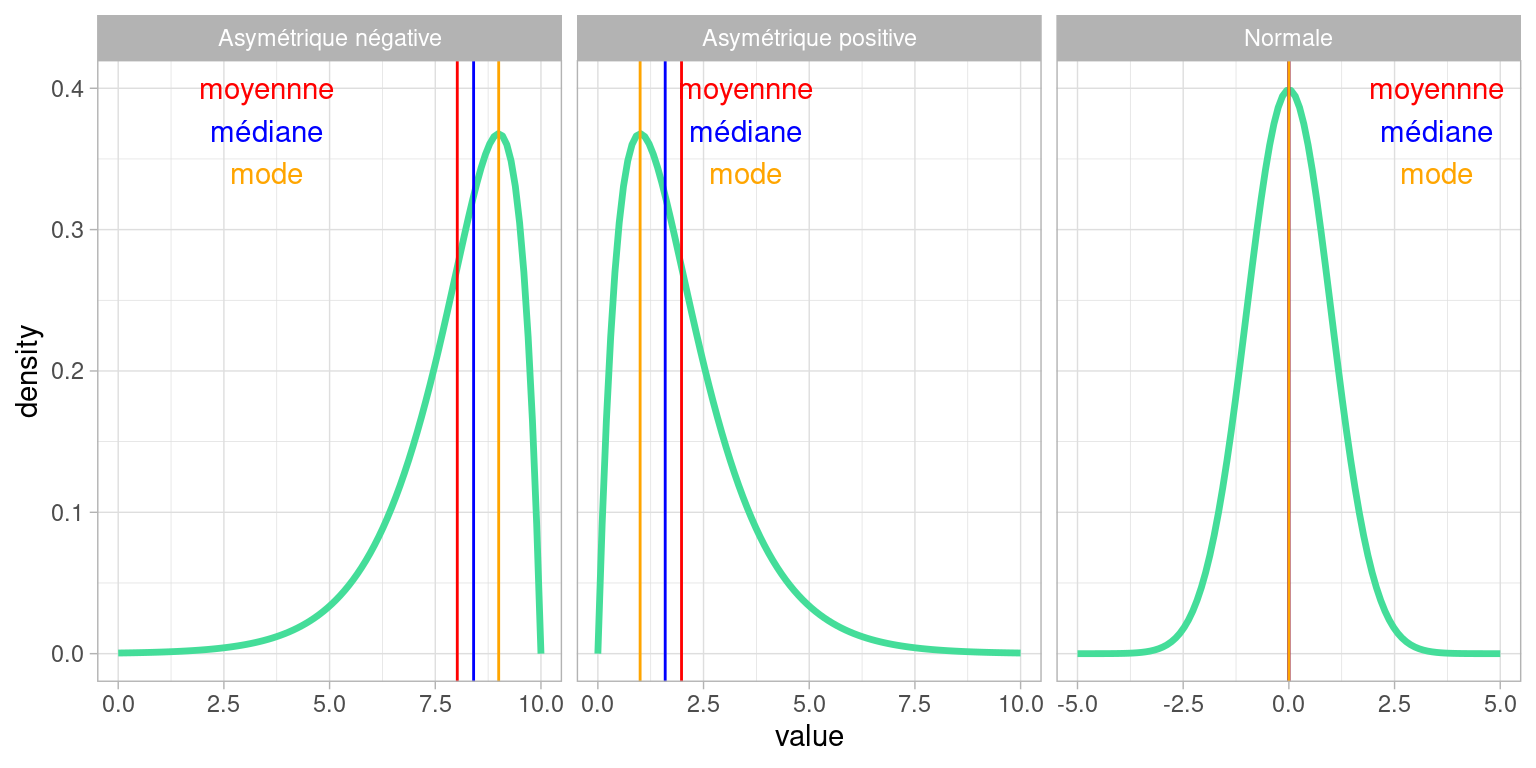
6.1.1 les Coefficients d’asymétrie de Pearson
Il existe deux mesures simples pour estimer l’asymétrie (skewness in english) d’une distribution d’une variable :
\(\displaystyle C_1 = \frac{\bar{x} - mode(X)}{\sigma_x}\)
et sa version “normalisée”
\(\displaystyle C_2 = \frac{3(\bar{x} - mediane(X))}{\sigma_x}\)
L’interprétation de ces coefficients est directe
- si le coefficient est nul, la distribution est symétrique
- si le coefficient est négatif, la distribution est déformée à gauche de la médiane (sur-représentation de valeurs faibles, à gauche)
- si le coefficient est positif, la distribution est déformée à droite de la médiane (sur-représentation de valeurs fortes, à droite)
6.1.2 Le coefficient d’asymétrie de Fischer
Ce coefficient est défini comme le moment d’ordre 3 de la variable \(X\) centrée réduite:
\(\displaystyle skewness'=\mathbb{E}\bigg[\bigg(\frac{X-\mu}{\sigma}\bigg)^3\bigg]=\frac{\sum_{i=0}^{n} (x_i - \mu)^3}{n\sigma^3}\)
avec \(X\) une variable de moyenne \(\mu\) et d’écart-type \(\sigma\).
Au passage :
- Centrer une variable, c’est lui soustraire sa moyenne.
- Réduire une variable, c’est la diviser par son écart-type.
- Vous connaissez déjà un «moment» , le moment d’ordre 2 : c’est la variance .
6.1.3 Calculer le coefficient d’asymétrie avec R
Nous utilisons la fonction skewness() du package moments et
library(moments)
skewness(iris$Sepal.Length)## [1] 0.31175316.2 L’Aplatissement (kurtosis)
L’ aplatissement d’une distribution , aussi appelée kurtosis quantifie la déviation de la forme de la distribution par rapport à une distribution normale.
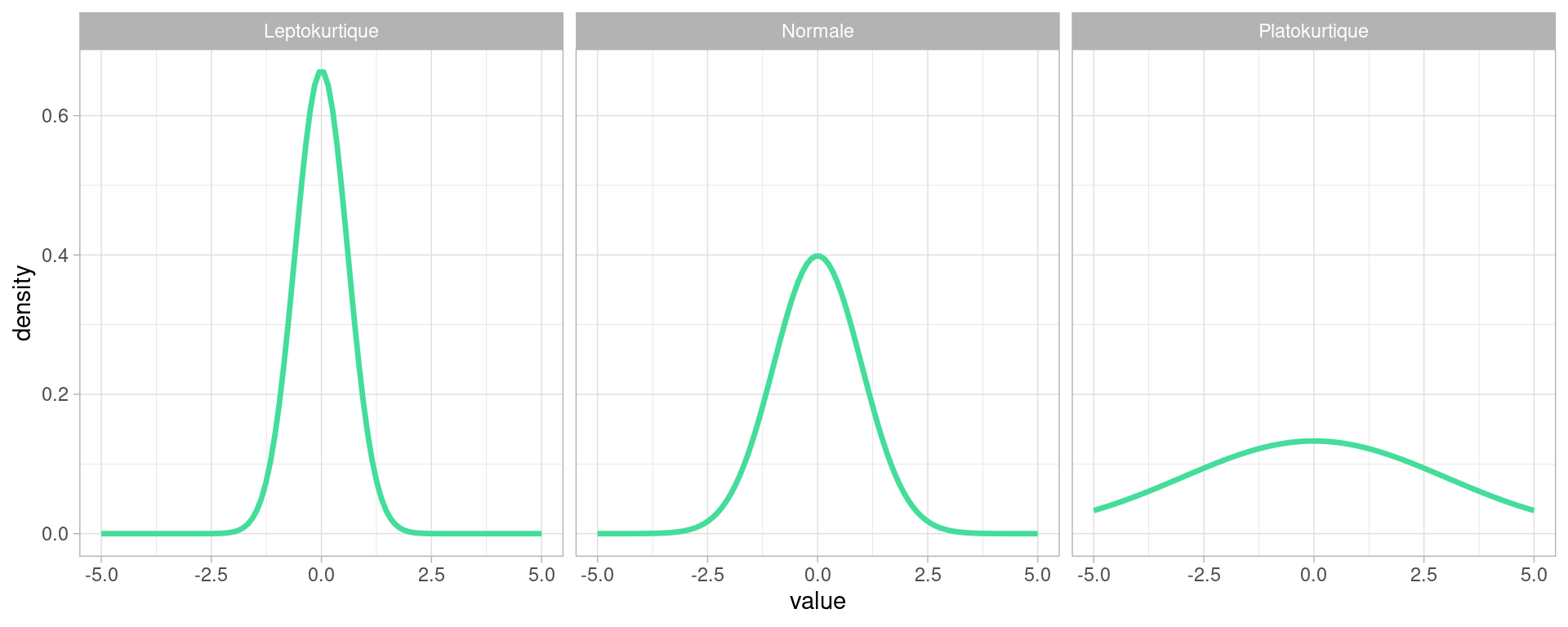
une courbe de distribution piquée indique peu de variations dans les valeurs, une distribution relativement homogène, avec beaucoup de valeurs égales ou proches de la moyenne.
La courbe aplatie suggère des variations importantes, une distribution relativement hétérogène, avec beaucoup de valeurs éloignées de la moyenne.
<<<<<<< HEAD6.2.1 Coefficient d’aplatissement (ou kurtosis)
le kurtosis d’une variable s’écrit :
\[K=\frac{\sum_{i=1}^{n}(x_i -\bar{x})^4}{n\sigma^4}\]
Si la distribution est normale , \(K= 3\)
Si \(K>3\), la distribution est plus applatie
Si \(K<3\), la distribution est moins applatie
On normalise parfois en considérant \(K'=K-3\) (qui mesure donc l’excès d’applatissement)
Au passage :
- on reconnait le moment statistiques d’ordre 4 dans l’équation de la kurtosis
- il s’agit de la version de Pearson
- cette mesure ne doit pas être confondue avec la dispersion. En pratique elle traduit plutôt l’existence d’outliers qui “étirent” la courbe de la distribution au delà d’un ou deux écarts-types , à droite et à gauche de la moyenne.
6.2.2 Exemple de distribution à écart-type faible, mais à kurtosis important
Il est tout à fait normal d’amalgamer dispersion et kurtosis en première approximation, puisqu’une distribution symétrique à fort écart-type sera plus aplatie qu’une distribution à symétrique à faible écart-type.
Il existe néanmoins des distributions à kurtosis élevé, sans pour autant que leur variance (ou écart-type ) le soit. Par exemple ,la distribution de Laplace :
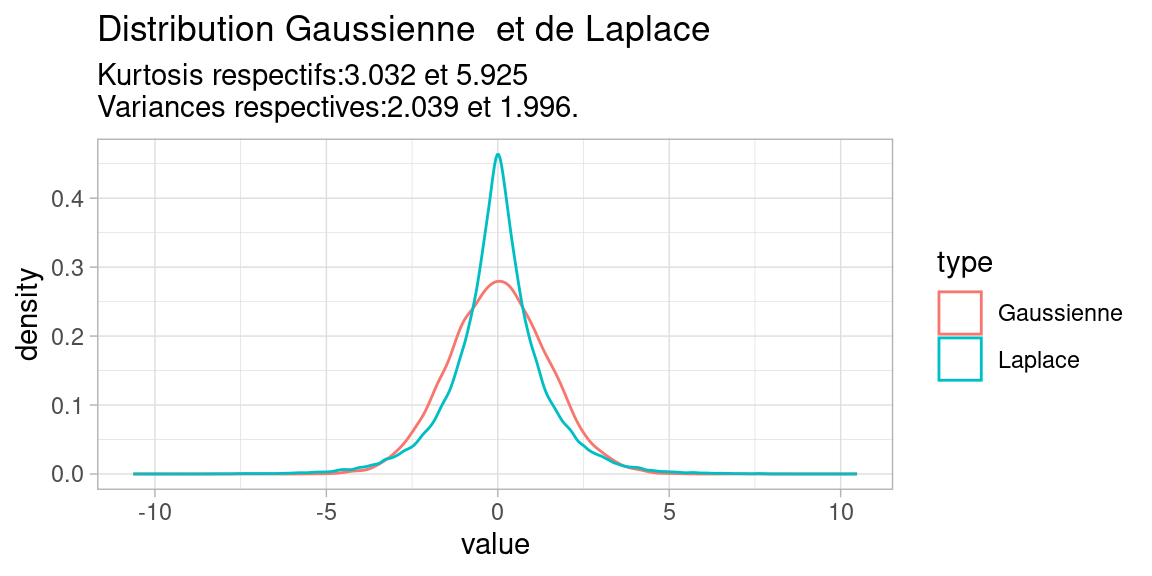
6.2.3 Calculer le kurtosis avec R
Nous utilisons la fonction kurtosis() du package moments et
library(moments)
kurtosis(iris$Sepal.Length)## [1] 2.4264326.3 Transformations des données
les distributions dont les formes sont particulièrement irrégulières sont délicates à appréhender (et représenter). Parfois, il est possible d’améliorer les choses en utilisant des transformations mathématiques.
\(x \mapsto log(x)\) pour une distribution asymétrique à droite ou \(x \mapsto \sqrt x\) si moins asymétrique (le logarithme «aplatit» les pics dus aux choses exponentielles)
\(x \mapsto x^2\) pour une distribution asymétrique à gauche ou \(x \mapsto x^3\) si très asymétrique . (Élever des choses au carré amplifie les petites valeurs))
Il faut toujours vérifier l’allure de la distribution transformée !
Une autre transformation courante est de centrer et réduire des variables. Centrer une variable signifie lui soustraire sa moyenne. Réduire une variable signifie la diviser par son écart-type.
Une variable centrée réduite est alors exprimée en «écarts-types à la moyenne»
- Cela permet de repérer les valeurs extrêmes (\(<2\sigma\) ou \(>2\sigma\)) , du moins si la distribution n’est pas trop irrégulière.
- C’est utile pour comparer des individus selon un grand nombre de variables
- Cela permet aussi de comparer des variables définies sur des intervalles de valeurs très différentes
6.4 Fat-tail distributions : un exemple
Les distributions très asymétriques et très étendues sont délicates à résumer.
Les indicateurs traditionnels sont plus efficaces lorsque la variabilité des valeurs est moindre, et leur distribution plus symétrique.
e.g. Considérer la population moyenne des villes de France a-t’elle du sens ?
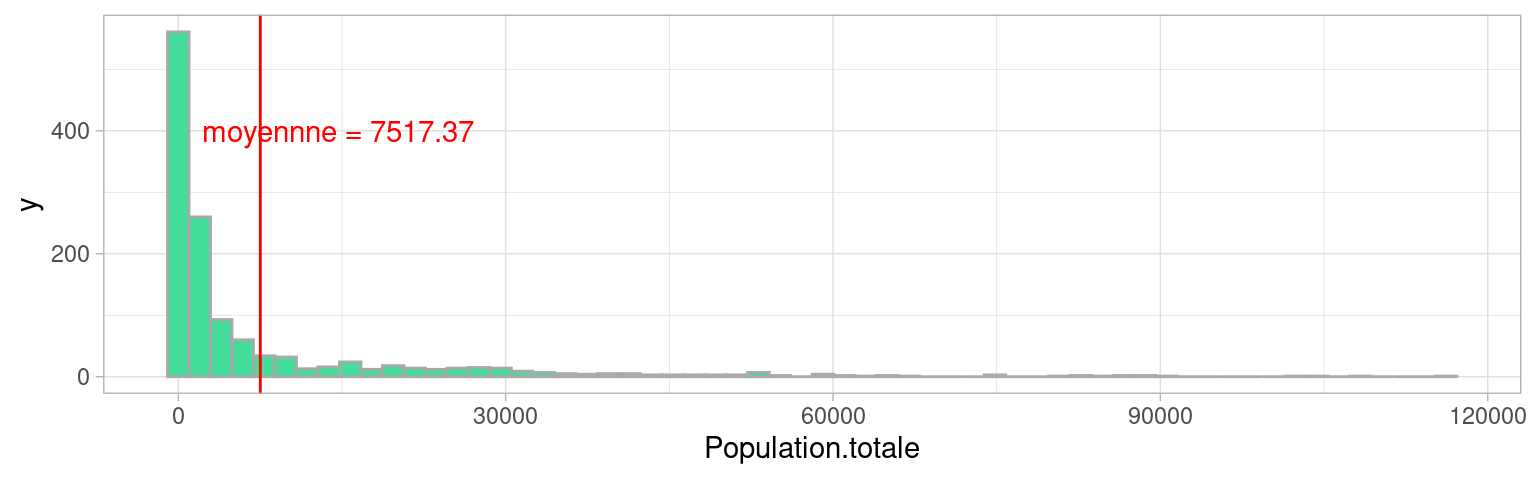
6.4.1 Distribution rang-taille des villes de france
Pour mieux voir la distribution et les écarts, on trace la taille des villes en fonction de leur rang
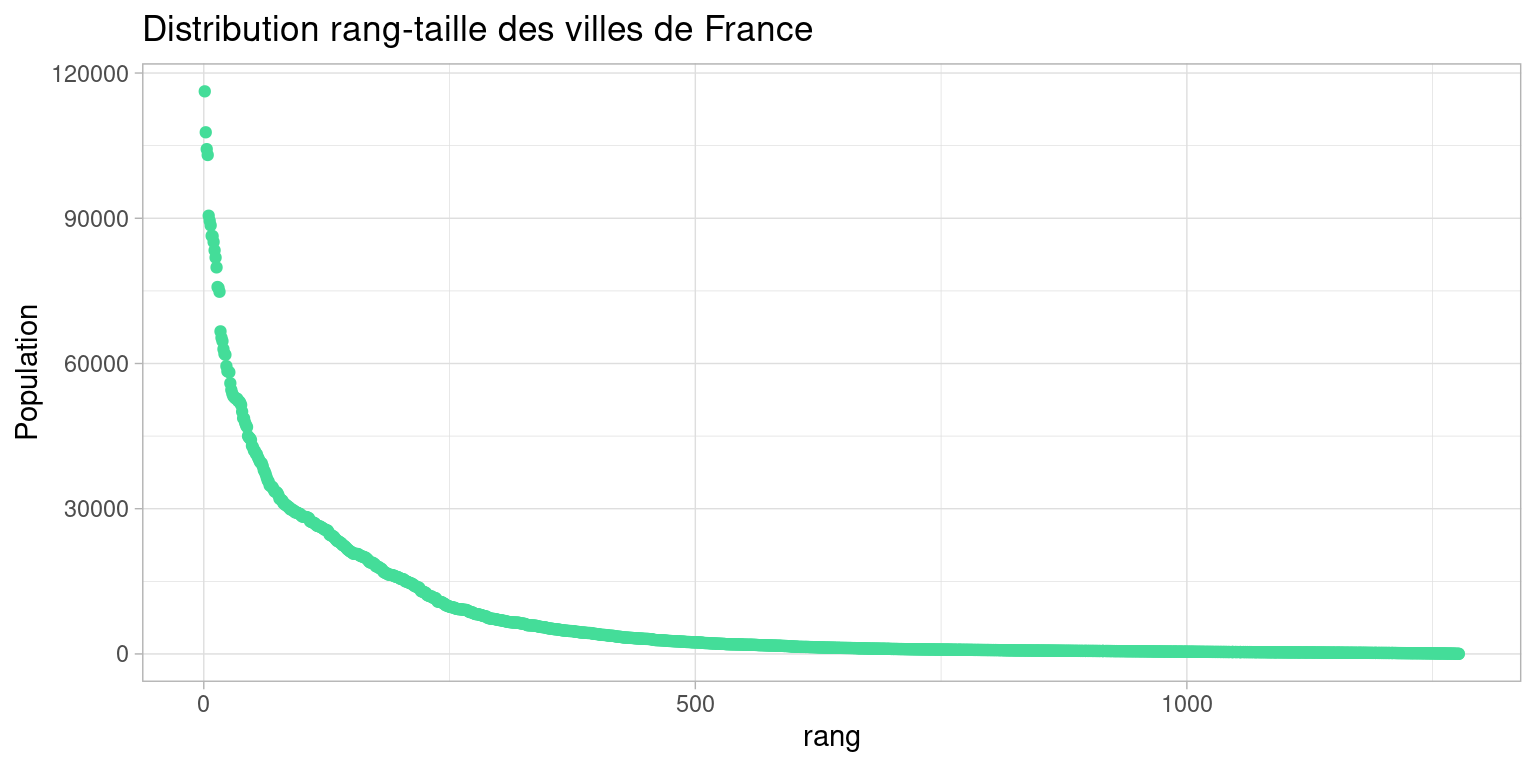
Lorsqu’on rencontre des distributions aussi piquée, on peut chercher à appliquer une transformation monotone, bijective et inversible qui “aplatisse” la distribution.
Cette transformation a pour objectif de
- réduire les écarts entre les valeurs
- resserrer la visualisation sur l’essentiel des valeurs
Cela aura aussi pour conséquence de mesurer façon plus robuste la tendance, dispersion et forme de la distribution (puisqu’elle sera moins éparpillée)
Ici, on choisit le logarithme décimal, qu’on va appliquer sur les ordonnées du graphique grâce à la fonction scale_y_log10()
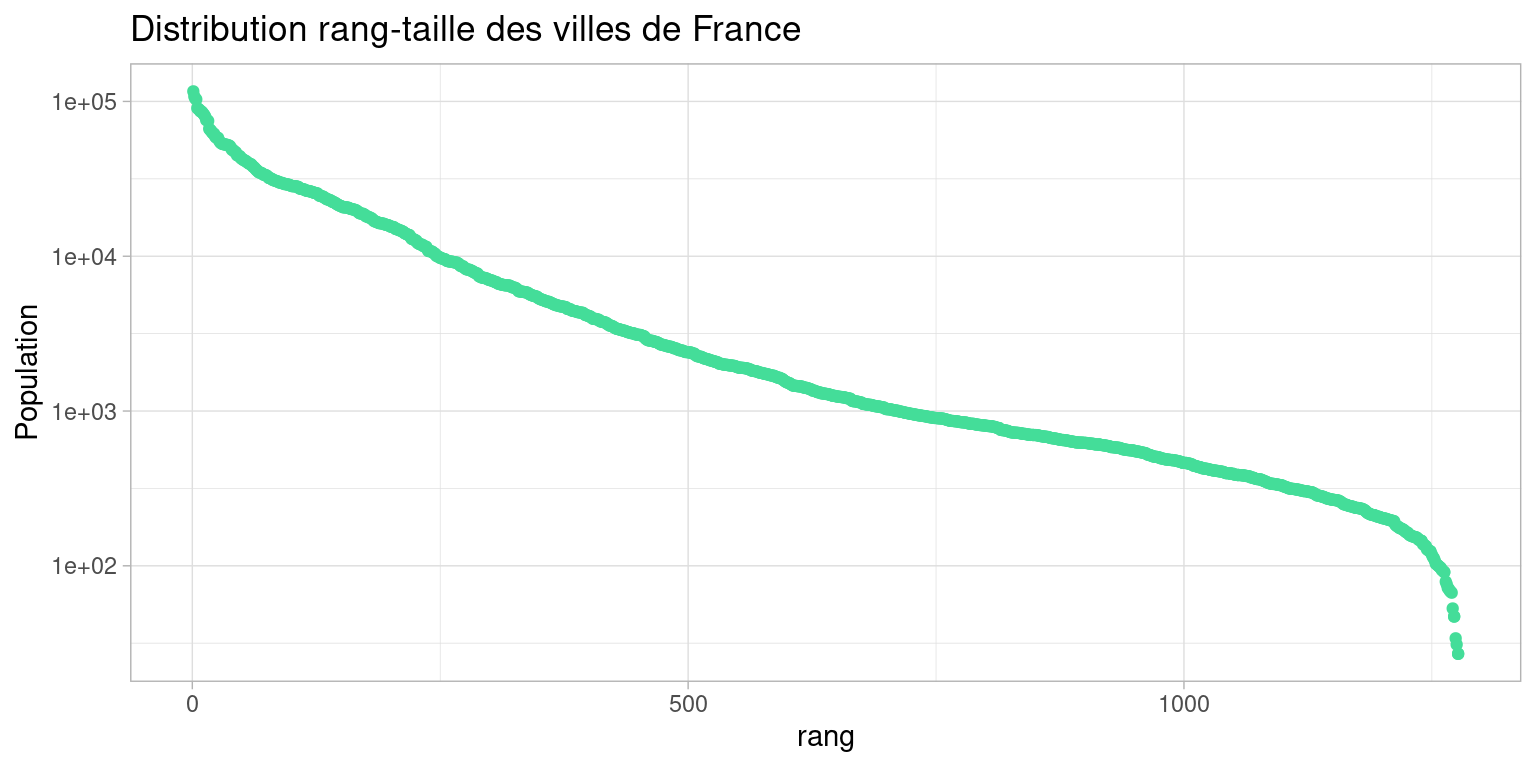
Cette transformation fait apparaître une régularité “linéaire” qu’il sera facile d’ajuster par une régression linéaire.
Cette représentation (dire “rang-taille”) et l’ajustement d’un modèle géométrique entre rang et taille, est très utilisée en géographie, et beaucoup de propriétés du système de villes (plus de détails à ce sujet : [https://www.hypergeo.eu/spip.php?article657]) dont on trace ainsi le profil s’y retrouvent : “âge” du système, déviation de certaines villes par rapport à la droite de la loi, longueur de la traîne formée par les petites villes, hiérarchisation du système, macrocéphalie etc…